THUPC2022 初赛 I 分组作业

班上 2n 个学生分成了 n 组，每组两个人。其中 1 号和 2 号为一组，3 号和 4 号为一组，……，2n-1 号和 2n 号为一组。

每个人决定是否愿意和队友合作，对于第 i 个学生，选择“愿意”会产生 c_i 的不满，选择“不愿意”会产生 d_i 的不满。

如果两名队友都选择“愿意”，那么根据实际情况他们可以合作或者不合作。但是如果有一名队友选择“不愿意”，那么他们只能不合作。

如果一个学生 i 选择了“愿意”但是他的队友选择了“不愿意”，那么他会因为队友产生 e_i 的不满。

学生中还有 m 个单向的喜欢关系，一个关系形如“A 喜欢 B”。在这样一个关系中，有两种情况（其中 i 表示第 i 个关系，且保证 A 和 B 不在同一组）：

  • 如果 A 没有和队友合作，且 B 选择了“愿意”，A 会有产生 a_i 的不满
  • 如果 A 表决了“不愿意”，但 B 成功与队友合作，那么 A 会产生 b_i 的不满。

问所有情况下最小的不满之和是多少。

n \leq 5000,m \leq 10000

解题思路：

场上这个题把队友演了，给队友磕个头

我们先考虑分组的部分，首先确定这个题的模型要最小化不满，那就应该是最小割。

对每一组建图，每个人建一个点，每个组建一个点：

  • 源点向每个人连一条容量为 d_i 的边，表示不愿意
  • 每个人向所在小组连一条容量为 c_i 的边，表示愿意
  • 每个小组再向每个人连一条容量为 \text{INF} 的边，表示给选了愿意的一条回退的路（最小割建图经典方法）
  • 两个人之间连边容量分别为 e_x,e_y 表示一方愿意但是另一方不愿意
  • 最后，每个小组向汇点连容量为 c_i 的边，表示双方合作

如图（图源官方讲评 PPT）：

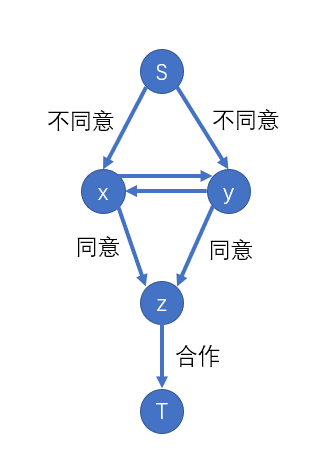
image-20220316172451486

这样的流一共有五种情况（图源官方讲评 PPT）：

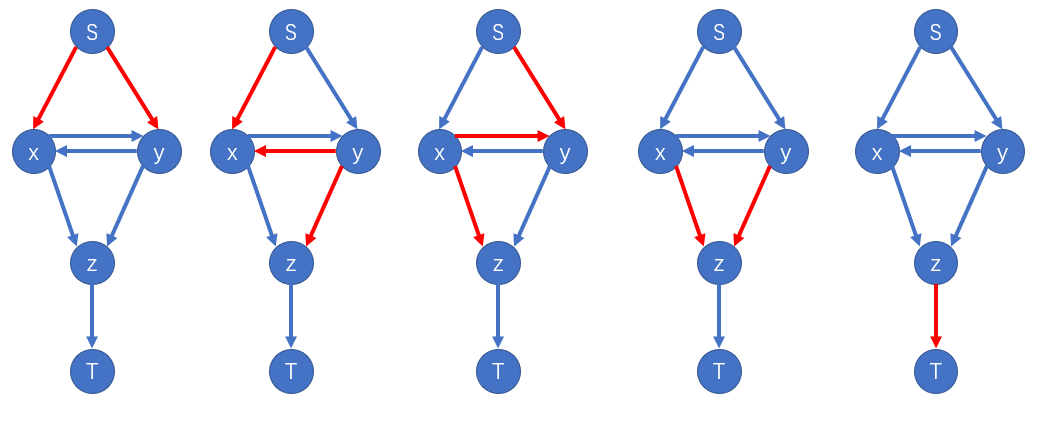
image-20220316172536632

第一种情况是双方均不愿意，第二/三种情况是 y/x 愿意但另一方不愿意。

这样我们就完成了没有喜欢关系的部分，喜欢关系的部分乍看之下需要拆点，实际上不用，对于一个喜欢关系我们可以这样建图：

  • 从 B 所在小组向 A 连容量为 b 边，表示 A 不愿意但是 B 合作了
  • 从 B 向 A 所在小组连容量为 a 边，表示 A 没有成功合作但是 B 愿意了。

这样我们就解决了本题。

代码：

const int N = 5e6 + 10;

struct edge {
    int cap,flow;
}e[N];

vector <pii> G[N];

int n,m,s,t,tot = -1,dis[N],cur[N];
bool vis[N];

bool BFS() {
    memset(dis,0,sizeof dis);
    memset(vis,0,sizeof vis);
    queue <int> q;
    q.push(s);dis[s] = 0;vis[s] = 1;
    while (!q.empty()) {
        int x = q.front();q.pop();
        for (auto ed : G[x]) {
            int y = ed.first,num = ed.second;
            if (!vis[y] && e[num].cap > e[num].flow) {
                vis[y] = 1;
                dis[y] = dis[x] + 1;
                q.push(y);
            }
        }
    }
    return vis[t];
}

int DFS(int x,int res) {
    if (x == t || res == 0) return res;
    int now = 0;
    for (int& i = cur[x];i < G[x].size();++i) {
        pii ed = G[x][i];
        int y = ed.first,num = ed.second;
        if (dis[x] + 1 == dis[y]) {
            int f = DFS(y,min(res,e[num].cap - e[num].flow));
            if (f > 0) {
                e[num].flow += f;
                e[num ^ 1].flow -= f;
                now += f;
                res -= f;
                if (!res) break;
            }
        }
    }
    return now;
}

int maxflow() {
    int ans = 0;
    while (BFS()) {
        memset(cur,0,sizeof cur);
        ans += DFS(s,0x3f3f3f3f3f3f3f3fLL);
    }
    return ans;
}

void addedge(int x,int y,int w) {
    G[x].push_back(mp(y,++tot));
    e[tot].cap = w;e[tot].flow = 0;
    G[y].push_back(mp(x,++tot));
    e[tot].cap = 0;e[tot].flow = 0;
}

signed main() {
    read(n,m);
    s = 0,t = 3 * n + 1; 
    for (int i = 1;i <= 2*n;++i) {
        int c,d,E;read(c,d,E);
        addedge(s,i,d);
        addedge(i,2 * n + ((i + 1) >> 1),c);
        addedge(2 * n + ((i + 1) >> 1),i,0x3f3f3f3f3f3f3f3fLL);
        addedge(2 * n + ((i + 1) >> 1),t,c);
        addedge(i,(i % 2 ? i + 1 : i - 1),E);
    }
    for (int i = 1;i <= m;++i) {
        int x,y,a,b;read(x,y,a,b);
        addedge(2 * n + ((y+1) >> 1),x,b);
        addedge(y,2 * n + ((x+1) >> 1),a);
    }
    printf("%lld\n",maxflow());
    return 0;
}