Kruskal 重构树学习笔记
做了 NOI2018 归程 学到的东西。
前置知识
- Kruskal 算法
- 一些数据结构基础
概念
Kruskal 重构树是一个基于 Kruskal 算法演变而来的图论算法,其用于解决一般图上诸如“只能经过边权小于等于某个值”相关问题。
Kruskal 算法的过程是将所有边进行排序,然后从小到大选择边,构建生成树。
Kruskal 生成树则是对于一条边
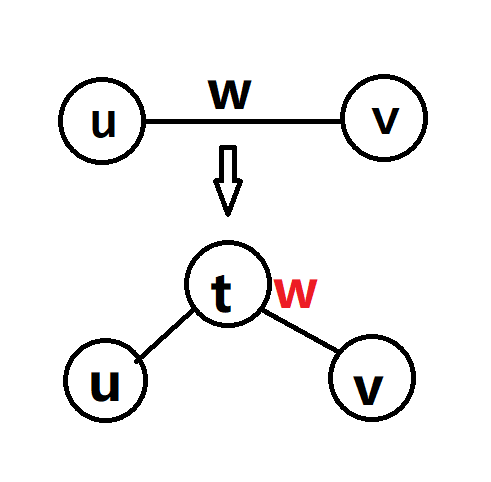
新的树有如下几个性质:
- 新的树满足二叉堆的性质
- 如果从大到小加边,整棵树是一个大根堆
- 任意两点之间的边权最大值是树上两点的 LCA
- 一个节点能走到的节点一定在它的子树中(会结合题目讲解)
给出建树的参考 Code:
int find(int x) {
return x == f[x] ? x : f[x] = find(f[x]);
}
void Kruskal() {
tot = n;
for (int i = 1;i <= m;++i) {
int fx = find(e[i].u),fy = find(e[i].v);
if (fx != fy) {
p[++tot] = e[i].w;
f[fx] = f[fy] = f[tot] = tot;
G[fx].push_back(tot);
G[tot].push_back(fx);
G[fy].push_back(tot);
G[tot].push_back(fy);
}
}
}例题
给一张无向图,最初你在点
x 并且有k 点社交牛逼值,你能从点i 获取a_i 点社交牛逼值,但是每个点只能获取一次。对于第i 条边有个限制w_i ,你至少要有w_i 点社交牛逼值才能牛逼到通过这条道路。有
q 组询问,每次询问给出x,k ,请求出你能获取的最大社交牛逼值。
n,m,q \leq 10^5
建出 Kruskal 重构树,那么这个题就等价于从点
Code:
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define mp make_pair
char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
int v = getchar();T f = 1;t = 0;
while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
read(t);read(args...);
}
const int N = 4e5 + 10;
vector <int> G[N];
int n,m,q,a[N],p[N],tot;
struct edge {
int u,v,w;
friend inline bool operator < (const edge &a,const edge &b) {
return a.w < b.w;
}
}e[N];
int f[N];
int find(int x) {
return x == f[x] ? x : f[x] = find(f[x]);
}
void Kruskal() {
tot = n;
for (int i = 1;i <= m;++i) {
int fx = find(e[i].u),fy = find(e[i].v);
if (fx != fy) {
p[++tot] = e[i].w;
f[fx] = f[fy] = f[tot] = tot;
G[fx].push_back(tot);
G[tot].push_back(fx);
G[fy].push_back(tot);
G[tot].push_back(fy);
}
}
p[0] = 0x3f3f3f3f;
}
int dep[N],siz[N],fa[30][N],val[30][N];
void dfs(int x,int fat) {
dep[x] = dep[fat] + 1;
for (auto y : G[x]) {
if (y != fat) {
dfs(y,x);
siz[x] += siz[y];
}
}
fa[0][x] = fat;
val[0][x] = p[fat] - siz[x];
}
void solve(int x,int k) {
for (int i = 20;i >= 0;--i) {
if (val[i][x] <= k && fa[i][x]) {
x = fa[i][x];
}
}
printf("%d\n",k + siz[x]);
}
signed main() {
read(n,m,q);
for (int i = 1;i <= n;++i) read(siz[i]),f[i] = i;
for (int i = 1;i <= m;++i) {
read(e[i].u,e[i].v,e[i].w);
}
sort(e+1,e+1+m);
Kruskal();
dfs(tot,0);
for (int i = 1;i <= 20;++i) {
for (int x = 1;x <= tot;++x) {
fa[i][x] = fa[i-1][fa[i-1][x]];
val[i][x] = max(val[i-1][x],val[i-1][fa[i-1][x]]);
}
}
//for (int i = 1;i <= tot;++i) printf("%d %d\n",siz[i],p[i]);
for (int i = 1;i <= q;++i) {
int x,k;read(x,k);
solve(x,k);
}
return 0;
}建立以海拔为关键字的 Kruskal 重构树(海拔为降序),那么能到达的点在 Kruskal 重构树的一个子树中。
那么就很清晰了,先用 Dijkstra 预处理单源最短路,再构建 Kruskal 重构树,然后 dfs 维护每个点为根的子树中距1号点的最小距离。处理询问时树上倍增即可。
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;
#define int long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define mp make_pair
char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
int v = getchar();T f = 1;t = 0;
while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
read(t);read(args...);
}
const int N = 1e6 + 10;
const int K = 26;
int n,m,q,k,s,dis[N],F[N],poi[N],val[N],tot,fat[N][K],f[N][K],dep[N];
bool vis[N];
vector <int> G[N];
vector <pii> G2[N];
struct edg {
int u,v,l,a;
friend inline bool operator < (const edg &A,const edg &B) {
return A.a > B.a;
}
}edge[N];
struct node {
int pos,d;
friend inline bool operator < (const node &a,const node &b) {
return a.d > b.d;
}
};
int find(int x) {return x == F[x] ? x : F[x] = find(F[x]);}
void clear() {
tot = n;
for (int i = 1;i <= (n << 1);++i) G[i].clear(),G2[i].clear(),F[i] = i;
}
void Dijkstra(int s) {
priority_queue <node> q;
memset(vis,0,sizeof vis);
memset(dis,0x3f,sizeof dis);
memset(val,0x3f,sizeof val);
q.push((node){s,dis[s] = 0});
while (!q.empty()) {
node p = q.top();q.pop();
int x = p.pos;
if (vis[x]) continue;
vis[x] = 1;
for (auto e : G2[x]) {
int y = e.first,w = e.second;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
q.push((node){y,dis[y]});
}
}
}
for (int i = 1;i <= n;++i) val[i] = dis[i];
}
void Kruskal() {
int cnt = 0;
for (int i = 1;i <= m;++i) {
int u = edge[i].u,v = edge[i].v,w = edge[i].a;
//printf("%d %d %d %d\n",u,v,find(u),find(v));
u = find(u),v = find(v);
if (u != v) {
++tot;poi[tot] = w;
//poi[u] = poi[v] = w;
F[u] = F[v] = tot;
val[tot] = 0x3f3f3f3f;
G[tot].push_back(u);
G[u].push_back(tot);
G[tot].push_back(v);
G[v].push_back(tot);
if (++cnt == (n - 1)) break;
}
}
}
void dfs(int x,int fa) {
fat[x][0] = fa;
dep[x] = dep[fa] + 1;
//printf("%d %d\n",fa,x);
for (int j = 1;j <= 20;++j) {
fat[x][j] = fat[fat[x][j-1]][j-1];
}
for (auto y : G[x]) {
if (y != fa) {
dfs(y,x);
val[x] = min(val[x],val[y]);
}
}
}
int query(int x,int y) {
for (int i = 20;i >= 0;--i) {
if (fat[x][i]) {
//printf("%d %d %d %d %d %d %d\n",x,dep[x],y,i,fat[x][i],poi[fat[x][i]],val[fat[x][i]]);
if (poi[fat[x][i]] > y) {
x = fat[x][i];
}
}
}
//printf("%d\n",x);
return val[x];
}
void solve() {
read(n,m);
clear();
for (int i = 1;i <= m;++i) {
read(edge[i].u,edge[i].v,edge[i].l,edge[i].a);
G2[edge[i].u].push_back(mp(edge[i].v,edge[i].l));
G2[edge[i].v].push_back(mp(edge[i].u,edge[i].l));
}
sort(edge + 1,edge + 1 + m);
Dijkstra(1);
//puts("here");
Kruskal();
//puts("here");
dfs(tot,0);
//puts("here");
read(q,k,s);
int lastans = 0;
for (int i = 1;i <= q;++i) {
int x,p;read(x,p);
x = (x + k * lastans - 1) % n + 1;
p = (p + k * lastans) % (s + 1);
printf("%lld\n",lastans = query(x,p));
}
}
signed main() {
int T;read(T);
while (T--) solve();
return 0;
}本作品采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。
评论已关闭