这建图，多是一件美事啊！

0.板子

本文中的所有建图思路均参考以下网络流板子实现，如有需要可直接复制。

最大流（使用 Dinic 算法实现）：

struct edge {
    int cap,flow;
}e[N];

vector <pii> G[N];

int n,m,s,t,tot = -1,dis[N],cur[N];
bool vis[N];

bool BFS() {
    memset(dis,0,sizeof dis);
    memset(vis,0,sizeof vis);
    queue <int> q;
    q.push(s);dis[s] = 0;vis[s] = 1;
    while (!q.empty()) {
        int x = q.front();q.pop();
        for (auto ed : G[x]) {
            int y = ed.first,num = ed.second;
            if (!vis[y] && e[num].cap > e[num].flow) {
                vis[y] = 1;
                dis[y] = dis[x] + 1;
                q.push(y);
            }
        }
    }
    return vis[t];
}

int DFS(int x,int res) {
    if (x == t || res == 0) return res;
    int now = 0;
    for (int& i = cur[x];i < G[x].size();++i) {
        pii ed = G[x][i];
        int y = ed.first,num = ed.second;
        if (dis[x] + 1 == dis[y]) {
            int f = DFS(y,min(res,e[num].cap - e[num].flow));
            if (f > 0) {
                e[num].flow += f;
                e[num ^ 1].flow -= f;
                now += f;
                res -= f;
                if (!res) break;
            }
        }
    }
    return now;
}

int maxflow() {
    int ans = 0;
    while (BFS()) {
        memset(cur,0,sizeof cur);
        ans += DFS(s,0x3f3f3f3f);
    }
    return ans;
}

void addedge(int x,int y,int w) {
    G[x].push_back(mp(y,++tot));
    e[tot].cap = w;e[tot].flow = 0;
    G[y].push_back(mp(x,++tot));
    e[tot].cap = 0;e[tot].flow = 0;
}

最小费用最大流（采用 Ford 算法实现）：

vector <pii> G[N];

struct edge {
    int from,cap,flow,cost;
}e[N];

int tot = -1,s,t;

void addedge(int u,int v,int w,int co) {
    e[++tot].cap = w;e[tot].cost = co;e[tot].flow = 0;e[tot].from = u;
    G[u].push_back(mp(v,tot));
    e[++tot].cap = 0;e[tot].cost = -co;e[tot].flow = 0;e[tot].from = v;
    G[v].push_back(mp(u,tot));
}

int dis[N],inq[N],p[N],aaa[N],n,m;

bool Ford(int &flow,int &cost) {
    memset(dis,0x3f,sizeof dis);
    memset(inq,0,sizeof inq);
    queue <int> q;
    dis[s] = 0;
    inq[s] = 1;
    p[s] = 0;aaa[s] = 0x3f3f3f3f;
    q.push(s);
    while (!q.empty()) {
        int x = q.front();q.pop();
        inq[x] = 0;
        for (auto now : G[x]) {
            int y = now.first;
            edge& edg = e[now.second];
            if (edg.cap > edg.flow && dis[y] > dis[x] + edg.cost) {
                dis[y] = dis[x] + edg.cost;
                p[y] = now.second;
                aaa[y] = min(aaa[x],edg.cap - edg.flow);
                if (!inq[y]) {
                    q.push(y);
                    inq[y] = 1;
                }
            }
        }
    }
    if (dis[t] == 0x3f3f3f3f) return 0;
    flow += aaa[t];cost += dis[t] * aaa[t];
    int x = t;
    while (x != s) {
        e[p[x]].flow += aaa[t];
        e[p[x] ^ 1].flow -= aaa[t];
        x = e[p[x]].from;
    }
    return 1;
}

pii MCMF() {
    int cost = 0,flow = 0;
    while (Ford(flow,cost));
    return mp(flow,cost);
} 

匈牙利算法：

int n,m,e,ans,match[N];
bool vis[N];
vector <int> G[N];

bool dfs(int x) {
    for (auto y : G[x]) {
        if (!vis[y]) {
            vis[y] = 1;
            if (!match[y] || dfs(match[y])) {
                match[y] = x;
                match[x] = y;
                return 1;
            }
        }
    }
    return 0;
}

int Hungary() {
    int ans = 0;
    for (int i = 1;i <= n;++i) {
        memset(vis,0,sizeof vis);
        if (dfs(i)) ++ans;
    }
    return ans;
}

1.基本建图

最简单的一类建图，通常就是题目给的边你把它按照要求建出来就好，就是纯考察板子的了。

例题：

P2756 飞行员配对方案问题

一共有 n 个飞行员，其中有 m 个外籍飞行员和 (n - m) 个英国飞行员，外籍飞行员从 1 到 m 编号，英国飞行员从 m + 1 到 n 编号。 对于给定的外籍飞行员与英国飞行员的配合情况，试设计一个算法找出最佳飞行员配对方案，使皇家空军一次能派出最多的飞机。

n,m \leq 100

没啥好说的，直接按照题目的给定要求飞行员建边即可。但是注意如果用 Dinic 返回路径可能不是很好写（其实也没多难），所以可以用匈牙利来实现。

2.最小割

在网络流里很重要的一个东西就是最小割，个人想先提一下这个东西以便于接下来的一些技巧的讲解。

首先引用一下 OI-wiki 里的定义：

割

对于一个网络流图 G=(V,E)，其割的定义为一种 点的划分方式：将所有的点划分为 S 和 T=V-S 两个集合，其中源点 s\in S，汇点 t\in T。

割的容量

我们的定义割 (S,T) 的容量 c(S,T) 表示所有从 S 到 T 的边的容量之和，即 c(S,T)=\sum_{u\in S,v\in T}c(u,v)。当然我们也可以用 c(s,t) 表示 c(S,T)。

最小割

最小割就是求得一个割 (S,T) 使得割的容量 c(S,T) 最小。

用这张图来理解，下图中灰色的点就是属于 S 的点，蓝色的点就是属于 T 的点，红色划掉的边就是这张图的一个割。

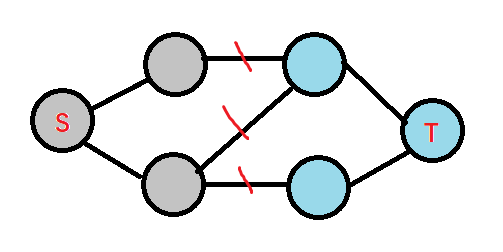
我们一般结合 最大流最小割定理 来对其相关问题进行求解。

定理：f(s,t)_{\max} = c(s,t)_{\min}

证明：考虑 u\in S,v \in T，(u, v) 一定满流，否则残余网络中存在 (u, v)，v 能被源点到达。

考虑 u \in S, v \in T,(v, u) \in E，(u, v) 一定没有流，否则残余网络中存在 (u, v)，v 能被源点到达。

那么 \sum _{u∈S,v∈T} (f(u, v) − f(v, u)) = \sum_{u∈S,v∈T} c(u, v)，即流量等于这个割的容量，且这个流是最大流。

这说明：不存在增广路的时候，流就是最大流。而最大流的时候，不存在增广路。

所以一个流是最大流当且仅当残余网络不存在增广路。同时这也给出了求最小割可行方案的方法。

用人话来说，想象一下如果一个流没有跑满的话，那么必定还有边是有剩余容量，那么就还可以流过去，也就是说没被割掉，S,T 之间还可以联通。而如果已经到了最大流的话，那么你考虑残量网络上一些边已经没有了，自然就把整个图给分成了两个点集。

最小割建图一般用在我们称作 二者选其一 的模型，一般如下：

有 n 个物品和两个集合 A,B，如果将一个物品放入 A 集合会花费 a_i，放入 B 集合会花费 b_i；还有若干个形如 u_i,v_i,w_i 限制条件，表示如果 u_i 和 v_i 同时不在一个集合会花费 w_i。每个物品必须且只能属于一个集合，求最小的代价。

首先我们建立源点与汇点 S,T，第 i 个点往 S 连一条 a_i 的边，表示选在 A 集合；往 T 连一条 b_i 的边，表示选在 B 集合。对于限制条件就在 u,v 之间连容量为 w 的边。如果源点汇点不相连的时候，我们就得到一组合法方案，对应了一组割。

如果把 S,T 与点的连边割掉，说明不选在这个集合。如果把 u,v 的边割掉，表示不放在一个集合里。

有时候我们在建图时，为了满足一些需求会连边权为无穷大的边，这里的边权就代表一种选择方案，不影响最小割（因为无穷大不可能在最小割方案中）但是提供了一种路径。

所以直接最大流即可。

例题 1：

P1361 小M的作物

小 M 在 MC 里开辟了两块巨大的耕地 A 和 B（你可以认为容量是无穷），现在，小 P 有 n 种作物的种子，每种作物的种子有 1 个（就是可以种一棵作物），编号为 1 到 n。

现在，第 i 种作物种植在A中种植可以获得 a_i的收益，在 B 中种植可以获得 b_i 的收益，而且，现在还有这么一种神奇的现象，就是某些作物共同种在一块耕地中可以获得额外的收益，小 M 找到了规则中共有 m 种作物组合，第 i 个组合中的作物共同种在 A 中可以获得 c_{1,i} 的额外收益，共同种在 B 中可以获得 c_{2,i}的额外收益。

小 M 很快的算出了种植的最大收益，但是他想要考考你，你能回答他这个问题么？

n \leq 10^3

就和上面讲的东西一样了，是板子题。但是注意这个组合的关系实际上是不太好处理的，所以可以额外建 m 个虚点，然后代表作物的点向虚点连一条容量为无穷大的边，代表选择这种方式，然后再从虚点往汇点连边。

例题 2：

P3973 [TJOI2015] 线性代数

给定一个 n \times n 的矩阵 B 和一个 1 \times n 的矩阵 C。求出一个 1×n 的 01 矩阵 A，使得 D=(A×B-C)×A^{\sf T} 最大，其中A^{\sf T}为A的转置，输出D。

直接看课件吧，写的很清楚了（

3.拆点

一般来说，对于拆点我们一个点都会有多个点，但是对于同一张图我们在编号的处理上为了避免错乱，本文推荐大家写一个类似如下的函数返回每个点在每个状态的编号，可以极大减少 Debug 工作量。

int gethash(int x,int y,int typ) {
    return typ * n * m + (x - 1) * m + y;
}
//Example
addedge(gethash(x,y,0),gethash(x,y,1),cap);

基础拆点

这部分拆点适用于一类给了你点权，却没有给边权的很讨厌的问题。

通常我们把这个点拆成一个入点和一个出点，在入点和出点间连容量为点权的边。

对于一条边 (u,v)，我们对于 (u,out) 与 (v,in) 之间连边。

以及有些题目会要求你去割点而不是割边，那么这样的题目我们把原本的 (u,v) 容量设为无穷大再跑最小割就是割点了。

例题：

P1345 奶牛的电信 Telecowmunication

John 的奶牛们喜欢通过电邮保持联系，于是她们建立了一个奶牛电脑网络，以便互相交流。这些机器用如下的方式发送电邮：如果存在一个由 c 台电脑组成的序列a_1,a_2,\cdots ,a_c，且 a_1 与 a_2 相连，a_2 与 a_3 相连，等等。那么电脑 a_1 和 a_c 就可以互发电邮。

很不幸，有时候奶牛会不小心踩到电脑上，农夫约翰的车也可能碾过电脑，这台倒霉的电脑就会坏掉。这意味着这台电脑不能再发送电邮了，于是与这台电脑相关的连接也就不可用了。

有两头奶牛就想：如果我们两个不能互发电邮，至少需要坏掉多少台电脑呢？请编写一个程序为她们计算这个最小值。

这个题就是刚才说的方法了，注意是双向边，所以要建两次。

按照约束拆点

这部分拆点适用于一类给了你每个点在某个状态，并且这个状态不是很大的时候的问题。

结合例题来讲吧。

P2754 [CTSC1999]家园 / 星际转移问题

现有 n 个太空站位于地球与月球之间，且有 m 艘公共交通太空船在其间来回穿梭。每个太空站可容纳无限多的人，而太空船的容量是有限的，第 i 艘太空船只可容纳 h_i 个人。每艘太空船将周期性地停靠一系列的太空站，例如 (1,3,4) 表示该太空船将周期性地停靠太空站 134134134\dots。每一艘太空船从一个太空站驶往任一太空站耗时均为 1。人们只能在太空船停靠太空站(或月球、地球)时上、下船。

初始时所有人全在地球上，太空船全在初始站。试设计一个算法，找出让所有人尽快地全部转移到月球上的运输方案。

1 \leq n \leq 13,1 \leq m \leq 20,1 \leq k \leq 50。

这题的建图就要按时间来考虑了，很明显的一点是，要把每一天都连向汇点然后求出总和。这个时候我们发现，如果其他的点仅仅只是一个点的话，无法满足求出每一天这个要求，因为会互相影响，这个时候我们就相应的把这些点拆成天数这么多个点，然后分别向向对应的天数连边。

源点向每一个星球一条容量为无穷大的边，每个空间站向下一时间的该空间站连一条容量为无穷大的边，代表时间间的转移。

每个飞船现在在哪个星球，下一秒会飞到哪一个星球都可以计算得到，所以直接连边，容量为飞船载人量。

然后就做完了，记得判断月球和地球是否联通即可。

4.二维类建图

这类建图有一种比较典型的套路。

染色连边

这种题的套路一般是让你在一个二维数组中选择一些元素，并且这些元素选择之间有一定的限制。通常连边方法就是把 i + j \bmod 2 \equiv 0 的格子染白，\equiv 1 的格子染黑，源点往白点，黑点往汇点连为点权的边。点与点之间通常跨黑白连边，按题目性质来连边权为无穷大的边即可。

例题1：

P2774 方格取数问题

有一个 m 行 n 列的方格图，每个方格中都有一个正整数。现要从方格中取数，使任意两个数所在方格没有公共边，且取出的数的总和最大，请求出最大的和。

n,m \leq 100

这题就是类似上边的方法，这里直接给出连边的代码。

s = n * m + 1,t = n * m + 2;
    for (int i = 1;i <= n;++i) {
        for (int j = 1;j <= m;++j) {
            read(a[i][j]);ans += a[i][j];
            if ((i + j) & 1) addedge(s,gethash(i,j),a[i][j]);
            else addedge(gethash(i,j),t,a[i][j]);
        }
    }
    for (int i = 1;i <= n;++i) {
        for (int j = 1;j <= m;++j) {
            for (int nxt = 0;nxt < 4;++nxt) {
                int nx = i + dx[nxt],ny = j + dy[nxt];
                if ((((nx + ny) & 1) == 0 &&  ((i + j) & 1) == 1) 
                    && nx <= n && ny <= m && nx > 0 && ny > 0) {
                    addedge(gethash(i,j),gethash(nx,ny),0x3f3f3f3f);
                }
            }
        }
    }

例题2：

P3227 HNOI2013 切糕

经过千辛万苦小 A 得到了一块切糕，切糕的形状是长方体，小 A 打算拦腰将切糕切成两半分给小 B。出于美观考虑，小 A 希望切面能尽量光滑且和谐。于是她找到你，希望你能帮她找出最好的切割方案。

出于简便考虑，我们将切糕视作一个长 P、宽 Q、高 R 的长方体点阵。我们将位于第 z 层中第 x 行、第 y 列上的点称 (x,y,z)，它有一个非负的不和谐值 v(x,y,z)。一个合法的切面满足以下两个条件：

• 与每个纵轴（一共有 P\times Q 个纵轴）有且仅有一个交点。即切面是一个函数 f(x,y)，对于所有 (x,y)(x\in [1,P],y\in[1,Q])，我们需指定一个切割点 f(x,y)，且 1\le f(x,y)\le R。

• 切面需要满足一定的光滑性要求，即相邻纵轴上的切割点不能相距太远。对于所有的 1\le x,x_1;\le P 和 1\le y,y_1;\le Q，若 |x-x_1;|+|y-y_1|=1，则 |f(x,y)-f(x_1,y_1)| \le D，其中 D 是给定的一个非负整数。

可能有许多切面 f 满足上面的条件，小 A 希望找出总的切割点上的不和谐值最小的那个。 P,Q,R \leq 40

首先按照套路，先把每个 (x,y) 拆成 R 个点，每个点之间连边为点权。题目很明显说了要你求最小割。

这题也是按照黑白染色的套路进行连边，对于光滑性的要求，我们不难发现从 i 往相邻格子 i-d 连一条容量为无穷大的边即可解决（为什么？请自行思考。Hint:根据最小割的性质）。

5.二分图

二分图似乎没有很必要介绍？节点由两个集合组成，且两个集合内部没有边的图。

接下来给出一些相关定理，有些较简单不给出证明。

最大匹配

将源点连上左边所有点，右边所有点连上汇点，容量皆为 1。原来的每条边从左往右连边，容量也皆为 1，最大流即最大匹配。

最小覆盖数

所有顶点中选择最少的顶点来覆盖所有的边。

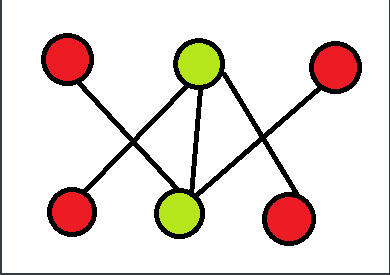
最大独立集

选最多的点，满足两两之间没有边相连。

二分图中，最大独立集 = n - 最大匹配。这个可以通过反证法。

证明：首先我们可以看出除了我们选择的两个用来最小覆盖的点之外，剩下的点之间彼此之间都没有连边，我们可以尝试把任意两个红点之间连一条边，那么明显，我们不满足最小覆盖的要求了，或者我们尝试通过转换使最小覆盖更小。当然不可行，因为我们已经求得就是最小覆盖了，并且易证的是剩下的所有点一定构成一个独立集。并且这个独立集的大小不能够更大了，然后我们就证出了题目所给的定理。

——摘自《最详细（也可能现在不是了）网络流建模基础 by victorique》

例题

P3355 骑士共存问题

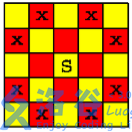
在一个 n \times n 个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入。

对于给定的 n \times n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击。

1 \leq n \leq 200，0 \leq m \lt n^2

首先先按照上面二维建图的套路，黑白染色拆点，发现这个题实际上就让我们求这个二分图的最大独立集。

这种有冲突关系的套路都是把冲突关系当成边来建，然后求独立集，注意这题 ban 掉的点不能选，建边的时候避开这些点就行。

DAG 最小路径覆盖

首先拆点，对于点 x 拆成 x_{in},x_{out} 两个点，对于一条边 (x,y) 把 x_{in} 向 y_{out} 连边，然后这样得到一个二分图。

答案就是原图的节点数 - 最大匹配。

证明的话感性理解下：一开始一共有 n 条不相交路径，每次合并一条路径，所以找到了多少条匹配边就算少了多少路径。

6.一些常用特殊性质图模型

最大权闭合子图

定义：闭合图一般指一个图中点的集合，从该集合中所有的点出发，能到达的点要求都必须在该点集中。

也就是说，从该集合中出发，一定要回到该集合中，不能出到集合外。通俗理解就是集合之间的点有关联性（可以类比有向图里的 DAG）。

最大权闭合子图，顾名思义，就是所有闭合子图中点权之和最大的那个，注意这里的权指的是点权，因为闭合图是对于点集而言的。

关于求解，可以直接套最小割的模型进行解决，源点向所有点权为正的点连容量为点权的边，所有点权为负的点连容量向汇点连为点权绝对值的边。然后求最小割，再用所有点权为正的权值之和减去最小割，就是我们要求的最大权值和了。

证明：

如何从最大权闭合子图转化到最小割的呢？首先我们要知道简单割的定义，简单割指的是割集的所有边都是从 s 出发的边或终点是 t 的边。

由此，我们知道在上述建图方式中的最小割一定是一个简单割，因为其图内部的边的流量是正无穷，所以最小割集一定不包含内部的边，是一个简单割。

然后我们需要证明闭合子图和简单割是一一对应的，从而我们求闭合子图的最值就是简单割的最小值，也就是建的新图的最小割。

我们假设一个闭合子图是 V，流网络分成两个集合 S 和 T，构成一个割集的情况。S 包含的是V + s （闭合子图的点+源点）；T包含的是剩下的所有点（闭合子图外的点+汇点）。

在这种情况下闭合子图 V 就和这个割[S，T]相对应，且这个割是个简单割。

这样我们就将闭合子图问题转化成了割的问题了，然后我们就要看看数量关系，找到最大权闭合子图和最小割间的数量表达式，就可以借助最小割模型计算最大权闭合子图了。 首先我们要找到最小割的计算表达式，下面是割集的所有情况：

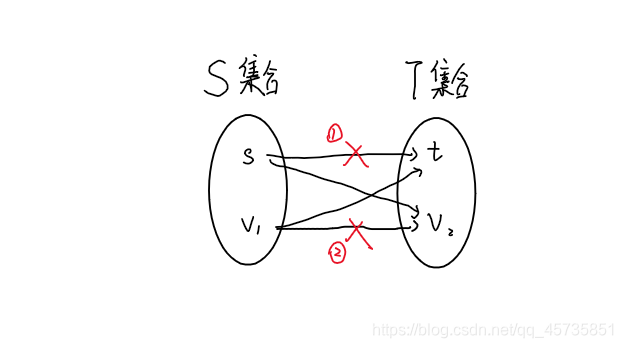
我们将原图中的点分为两个集合，V_1 和 V_2，V_1 是闭合子图的点集，V_2是原图中剩下的所有点，割集就只剩两种情况 s 到 V_2 和 V_1 到 T ,根据建图方式可得：前者的容量和是 V_2 中所有点权为正的和，后者容量和是 V_1 中所有点权为负数的和的相反数，割集的容量之和就是 V_2 中所有点权为正的和 + V_1 中所有点权为负数的和的相反数。

然后我们再看我们要求的闭合子图权值之和的计算表达式：最大权值和就等于 V_1 中所有的权值和，即 V_1 中所有点权为正的和 + V_1中所有点权为负的和。

我们将上面求出来的两个表达式相加可得：割集容量之和+闭合子图权值之和=原图中所有点权为正数的点权之和（后面的相加后刚好抵消）。而等式的右边是个定值，我们为使闭合子图权值最大化，所以我们就要使得割集容量之和最小化，即求最小割的大小，再用所有点权为正的权值之和减去最小割，就是我们要求的最大权值了。

参考自：CSDN博主「harry1213812138」的原创文章

一般这种模型就适合投入 x_1 \dots x_k 能带来 y 的产出，且这些 x 只用选择一次这类的题目。

例题：

P4174 NOI2006 最大获利

在前期市场调查和站址勘测之后，公司得到了一共 N 个可以作为通讯信号中转站的地址，而由于这些地址的地理位置差异，在不同的地方建造通讯中转站需要投入的成本也是不一样的，所幸在前期调查之后这些都是已知数据：建立第 i 个通讯中转站需要的成本为 P_i（1 \leq i \leq N）。

另外公司调查得出了所有期望中的用户群，一共 M 个。关于第 i 个用户群的信息概括为 A_i，B_i 和 C_i ：这些用户会使用中转站 A_i 和中转站 B_i 进行通讯，公司可以获益 C_i。（1 \leq i \leq M，1 \leq A_i，B_i \leq N）

THU 集团的 CS&T 公司可以有选择的建立一些中转站（投入成本），为一些用户提供服务并获得收益（获益之和）。那么如何选择最终建立的中转站才能让公司的净获利最大呢？（净获利 = 获益之和 – 投入成本之和）

N \leq 5000,M \leq 5\times 10^4

这个题把用户群当成权值为正的点，把中转站当成权值为负的点，如上建图即可。注意源点一定要连到权值为正的，不要搞反了。

结语

推荐练习

以上就是网络流建图的基本思想了，接下来可以进行更多的练习。个人推荐以下题单：

网络流建模经典题 By feecle6418

网络流 24 题

参考

最详细（也可能现在不是了）网络流建模基础 - ~victorique~

OI-Wiki

感谢以上内容提供方。