2011 ACM-ICPC World Finals 解题报告

WF 不愧是 WF，眼高手低人被打成粉末。

[TOC]

A

有两种操作：

A 操作：将当前数加 a

M 操作：将当前数乘 m

给出 a,m ，构造一个操作序列，将 [p,q] 中的每个数变换为 [r,s] 中的一个数。在此基础上最小化长度，在此基础上最小化字典序。

a,m,p,q,r,s\leq 10^9。

显然的观察是，M 操作是 \log 级别的了。

那么你考虑 [p,q] 里面如果我们能把 p 给转化到 [r,s]，则必定可以利用某个操作序列转化其他的到 [r,s] 里面。

这是本题第一个关键点，第二个关键点是，我们怎么处理 A 操作？

观察可得，我们可以把最终的 p 表示为 p=a\times (m^{P_1}+ m^{P_2}+\dots +m^{P_n}) 的形式，这样实际上是构造了一个 m 进制的数，所以我们要确定的也就是 P_1\dots P_n。

首先我们需要保证 n 最小，也就是这个数每位上的数字和最小。从高位枚举下来，贪心处理。时间复杂度不太会算，但是能过。

思考题

有一个不知道次数的 f(x) = \sum_{k=0}^n a_kx^k(a_i\in \N),用最小次数将每个 a_i 求出来。

和上面一样的思路，其实只要两次就能求出来了。第一次求出来 f(1) = \sum_{k = 0}^n a_k,算 f(f(1)) 实际上就表示出来一个 f(1) 进制的数。

C

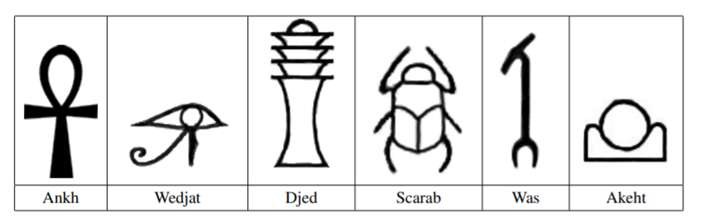
有六种远古符号如图所示：

给出一张像素图，判断图中写的是哪种符号。

n,m\leq 200

这个题观察到直接搜轮廓其实是很不好搜的，转化一下问题，与其搜黑色的连通块不如搜白色的连通块。

这边就需要一点观察了，这六个图形中完全包含的白色部分分别有 1，3，5，4，0，2 个，于是你做一下搜索就写完了，实际上可能并没有那么好写

E

平面上有 n 个咖啡店，q 次询问，每次询问如下：

找一个点，距离其曼哈顿距离不超过 m 的咖啡店最多。

n\leq 500000,q\leq 20,坐标范围 [1,1000]。

注意到这个题其实没有那么简单，因为这个形成的图由若干个翻转 45 ° 的矩形组成，大致是这样的。

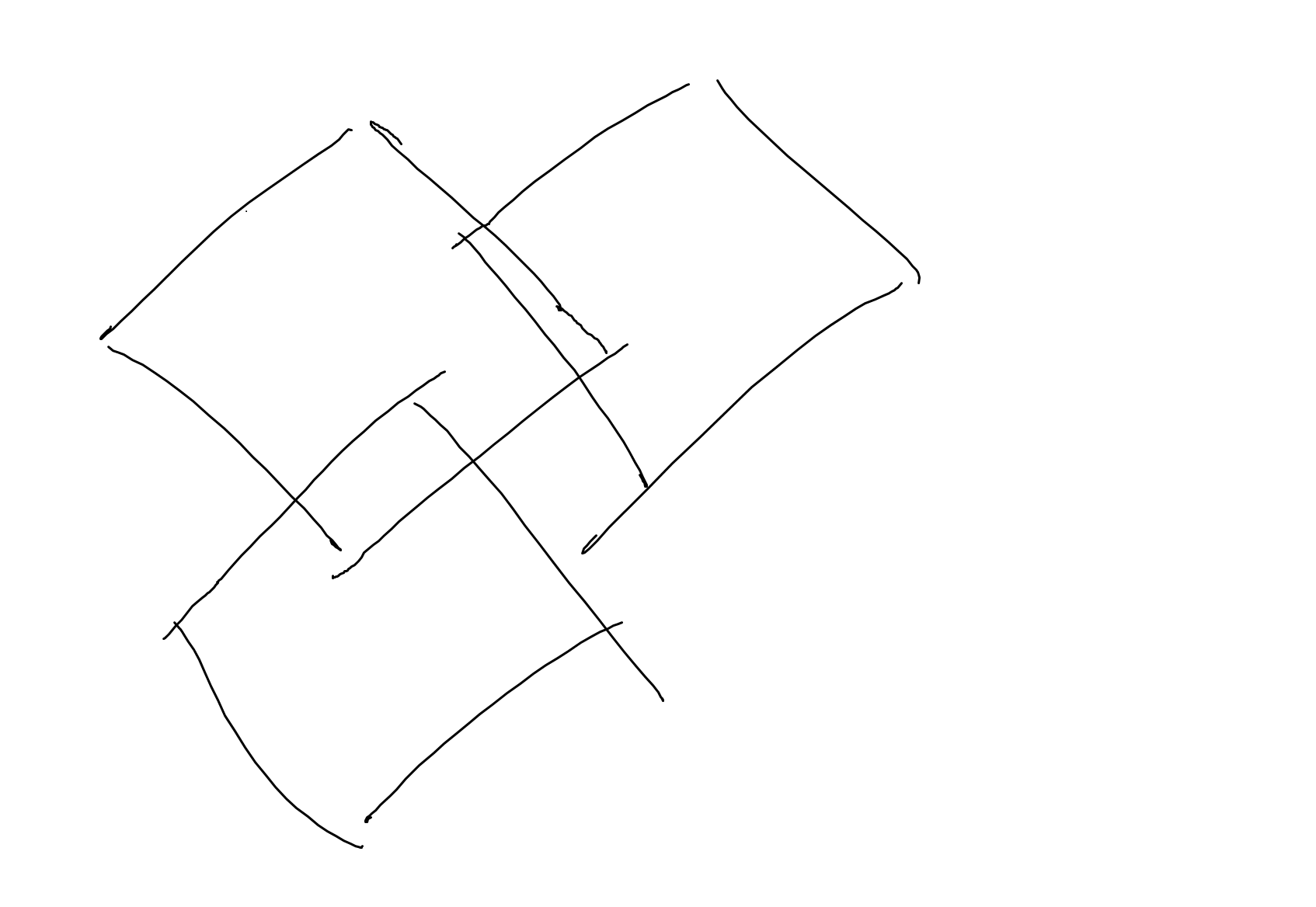
斜的图我们实际上非常讨厌，因为没有办法很快计算。

所以我们采用一个将曼哈顿距离转化为切比雪夫距离的方法，将整张图变成若干个矩形的经典样式，然后发现坐标范围只有 [0,1000] 直接大力选出交集最多的矩形即可。

时间复杂度 O(nm)

Code:

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
using namespace std;
#define ll long long
#define ri int
#define int long long

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    ri v = getchar();T f = 1;t = 0;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
    t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
    read(t);read(args...);
}

const int N = 5e5 + 10;

struct poi {
    int x,y;
}p[N];

int dx,dy,n,m,sum[2010][2010],ma[2010][2010];

void solve(int qwq) {
    int ans = 0,posx,posy;
     for (int j = 1;j <= dy;++j) {
        for (int i = 1;i <= dx;++i){
            int x = i + j - 1,y = i-j + dy;
            int x1 = max(1ll,x - qwq),x2 = min(dx + dy - 1,x + qwq );
            int y1 = max(1ll,y - qwq),y2 = min(dx + dy - 1,y + qwq);
            if (sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1 - 1][y1 - 1] > ans) {
                ans = sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1 - 1][y1 - 1];
                posx = i,posy = j;
            } else if (sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1 - 1][y1 - 1] == ans) {
                if (posy > j) {
                    posx = i,posy = j;
                } else if (posy == j && posx > i) {
                    posx = i,posy = j;

                }
            }
        }
    }
    printf("%lld (%lld,%lld)\n",ans,posx,posy);
}

signed main() {
    int $ = 0;
    while (1) {
        memset(ma,0,sizeof ma);
        memset(sum,0,sizeof sum);
        read(dx,dy,n,m);
        if (dx == 0 && dy == 0 && n == 0 && m == 0) return 0;
        printf("Case %d:\n",++$);
        for (int i = 1;i <= n;++i) {
            int x,y;read(x,y);
            p[i].x = x+y-1,p[i].y = x-y+dy;
            //printf("%d %d\n",p[i].x,p[i].y);
            ma[p[i].x][p[i].y]=1;
        }
        for (int i = 1;i <= dx + dy - 1;++i) {
            for (int j = 1;j <= dx + dy - 1;++j) {
                sum[i][j] += sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + ma[i][j];
                //printf("%d ",sum[i][j]);
            }
            //puts("");
        }
        while (m--) {
            int x;read(x);
            solve(x);
        }
    }
    return 0;
}

F

若干台机器，你可以在 d_i 天以 p_i 的价格买入第 i 台机器（钱不够买不了），在下一天开始运行它，每天产生 g_i 利润，并且可以选择随时将其卖出去得到 r_i元。

初始你有 c 元，一共有 d 天，结束时卖出所有机器。求最多能获得多少利润。

n\leq 10^5

f_i= \max_{1\leq j < i}\{f_j + g_i * (d_i - d_j) + r_j - p_i\}(r_j - p_i + now \geq 0)\\

斜率优化，CDQ分治维护凸壳

没有 code 因为我不会写

G

给出若干根首尾相接的火柴。

允许将其拆分后围成多边形，最大化围成的面积。

n\leq 500

没有 code 因为我不会写

H

有 n 个矿井，由 m 个隧道连接。

现在要在某些矿井安装逃生通道，使得任何一个矿井发生坍塌的时候，其余矿井的人都能逃到地面。

求最小的通道数量，以及最优方案数。

n,m\leq 5\times 10^4

经典题。

首先我们考虑割点被炸掉的情况，似乎我们只需要在每个点双连通分量里面做一个通道数就可以了。

但是如下这个图可以 hack 掉这个做法

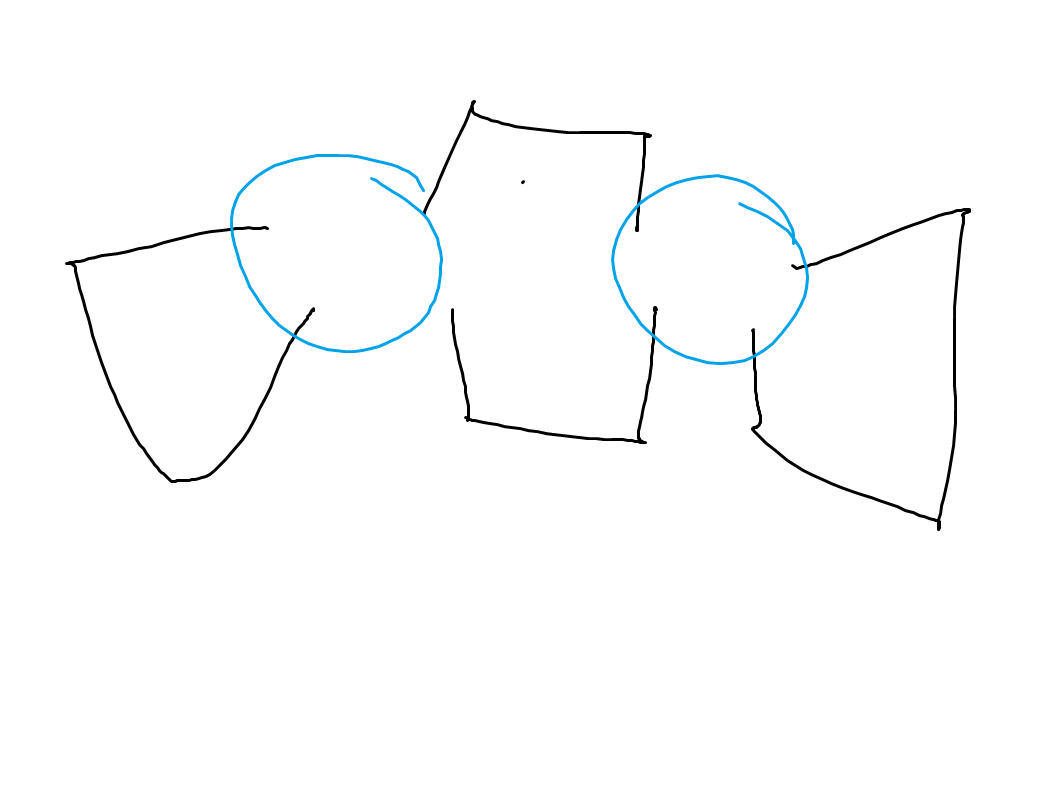
蓝色为割点，黑色为点双联通分量。

那么因为只炸掉一个点，所以两个割点任意炸掉一个另外两个点双都是可以互相到达的，只要建一个就行。

所以我们注意到，如果一个点双里面只存在一个割点，那么必须在这个点双加上一个通道，否则就不用。

注意特判掉只有一个点双（一个环）的情况。

这里我们可以引出一个数据结构：圆方树。

众所周知边双是可以直接把桥当成树边缩点为一棵树的，但是点双由于会产生一个割点在多个点双里的情况，所以不能直接缩点。

我们考虑把所有割点提出来，往它所在的所有点双连边，点双之间连边，这样就形成了一颗树。

这棵树我们叫其圆方树，一张著名的图可以阐述名字来源。

那么这个题就变成了圆方树叶子节点个数。

时间复杂度 O(n)

Code:

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
using namespace std;
#define ll long long
#define ri int

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    ri v = getchar();T f = 1;t = 0;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
    t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
    read(t);read(args...);
}

const int N = 5e4 + 10;

ll T,m,n,dfn[N],low[N],cnt,num,s[N],top,c,nn,bcc[N];
ll ans1,ans2;
bool cut[N];

vector <int> G[N];

void init() {
    ans1 = 0; ans2 = 1;
    for (int i = 1;i < N;++i) {
        G[i].clear();cnt = 0;
        dfn[i] = 0;cut[i] = 0;low[i] = 0;bcc[i] =  0;
    }
}

void tarjan(int x,int anc) {
    dfn[x] = low[x] = ++cnt;
    int isroot = 0;
    for (auto y : G[x]) {
        if (!dfn[y]) {
            tarjan(y,anc);
            low[x] = min(low[x],low[y]);
            if (low[y] >= dfn[x]) {
                ++isroot;
                if (x != anc || isroot > 1) {
                    cut[x] = 1;
                }
            }
        } else {
            low[x] = min(low[x],dfn[y]);
        }
    }
}

void dfs(int x,int col) {
    bcc[x] = col;++nn;
    for (auto y : G[x]) {
        if (cut[y] && bcc[y] != col) {
            ++c;
            bcc[y] = col;
        }
        if (!bcc[y]) {
            dfs(y,col);
        }
    }
}

void solve() {
    printf("Case %d: ",++T);
    n = 0;
    init();
    for (int i =1;i <= m;++i) {
        ll x,y;read(x,y);
        n = max(n,x);n = max(n,y);
        G[x].push_back(y),G[y].push_back(x);
    }
    for (int i = 1;i <= n;++i) {
        if (!dfn[i]) s[top=1] = i,tarjan(i,i);
    }
    //printf("%d\n",n);
    for (int i = 1;i <= n;++i) {
        if (!bcc[i] && !cut[i]) {
            c = nn = 0;
            dfs(i,++num);
            if (c == 1) ++ans1,ans2 *= nn;
            else if (!c) ans1 += 2,ans2 *= (nn-1)*nn/2;
        }
    }

/*
    for (int i = 1;i <= num;++i) {
        int tot = 0;
        for (auto x:bcc[i]) {
            tot += cut[x];
        }
        if (tot == 1) ++ans1,ans2 += bcc[i].size() * (bcc[i].size() - 1) / 2;
        if (!tot) ++ans1,ans2 += bcc[i].size();
    } */
    printf("%lld %lld\n",ans1,ans2);
}

signed main() {
    while (1) {
        read(m);
        if (m) solve();
        else break;
    }
    return 0;
}

J

有 c 块砖，你可以摆出两种类型的金字塔：

n\times n，(n-1)\times(n-1)，…

n\times n，(n-2)\times (n-2)，…

你需要恰好用完这些砖，最小化堆成的金字塔的数量，在此基础上最大化最大金字塔，在此基础上最大化第二大的金字塔，……

c \leq 10^6，Time Limit:10s

诈骗题。

我们考虑将第一个式子化一下 \sum_{i=0}^{n-1} (n-i)^2 = \frac{n\times(n+1)\times(2n+1)}{6}

所以我们可以搭的金字塔个数在 O(n^{\frac{1}{3}}) 级别的，大约是 300

所以直接跑一个 01 背包即可，时间复杂度 O(ct)，t为物品数，注意是 10 秒，所以能过。

Code:

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
using namespace std;
#define ll long long
#define ri int

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    ri v = getchar();T f = 1;t = 0;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
    t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
    read(t);read(args...);
}

const int N = 1e6+10;
const int K = 330;

int f[N],n;
bool road[N][K];

struct node {
    int v,w,typ,num;
    friend inline bool operator < (node a,node b) {
        return a.v < b.v;
    }
}a[K];

signed main() {
    //freopen("fuck.txt","w",stdout);
    //freopen("qwq.txt","r",stdin);
    int $ = 0;
    int tot = 0,cnt = 2;
    n = 1000000;
    for (int i = 2,sum = 1;sum <= n;i ++) {
        //printf("%d\n",sum);
        sum += i * i;
        a[++tot].v = sum;a[tot].typ = 1;a[tot].num = i;
    }
    for (int i = 3,sum = 1;sum <= n;i += 2) {
        //printf("%d\n",sum);
        sum += i * i;
        a[++tot].v = sum;a[tot].typ = 2;a[tot].num = i;
    }
    for (int i = 4,sum = 4;sum <= n;i += 2) {
        sum += i * i;
        a[++tot].v = sum;a[tot].typ = 2;a[tot].num = i;
        //printf("%d\n",sum);
    }
    //puts("here");
    //printf("%d\n",tot);
    sort(a+1,a+1+tot);
    memset(f,0x3f,sizeof f);
    f[0] = 0;
    int qwq = 0;
    for (int i = 1;i <= tot;++i) {
        qwq += a[i].v;
        //printf("%d ",qwq);
        if (qwq > 1000000) qwq = 1000000;
        for (int j = qwq;j >= a[i].v;--j) {
            //printf("%d ",j);
            if (f[j-a[i].v]+1 <= f[j]) {
                road[j][i] = 1;
                f[j] = min(f[j],f[j-a[i].v] + 1);
            }
            //printf("%d %d\n",i,j);
        }
    }
    //for (int i = tot-10;i <= tot;++i) printf("%d %d %d\n",a[i].v,a[i].typ,a[i].num);
    while (~scanf("%d",&n)){
        if (n == 0) break;
        printf("Case %d: ",++$);

        //cout << f[n] << endl;
        if (f[n] == 0x3f3f3f3f) {
            puts("impossible");
            continue;
        }
        int now = n;
        //while (now){
        for (int i = tot;i;--i) {
            if (road[now][i]) {
                printf("%d",a[i].num);
                if (a[i].typ == 1) putchar('H');
                else putchar('L');
                now -= a[i].v;
                putchar(' ');
            }
        }
        //}
        puts("");

    }
    return 0;
}

I

平面上有 n 个木乃伊在追你

在你的回合，你能朝上下左右走一步。

在木乃伊的回合，他们会朝着离你最近的坐标轴方向走一步。

求最多可以支撑几个回合，或是可以逃走。

n\leq 100000

首先让你求最多，我们考虑这个可以支撑的回合显然是有单调性的，考虑二分。

我们接着考虑如何 check，假设当前在 m 回合，我们显然可以把木乃伊追到人的范围画成一个矩形，再把我自己画一个矩形，如图

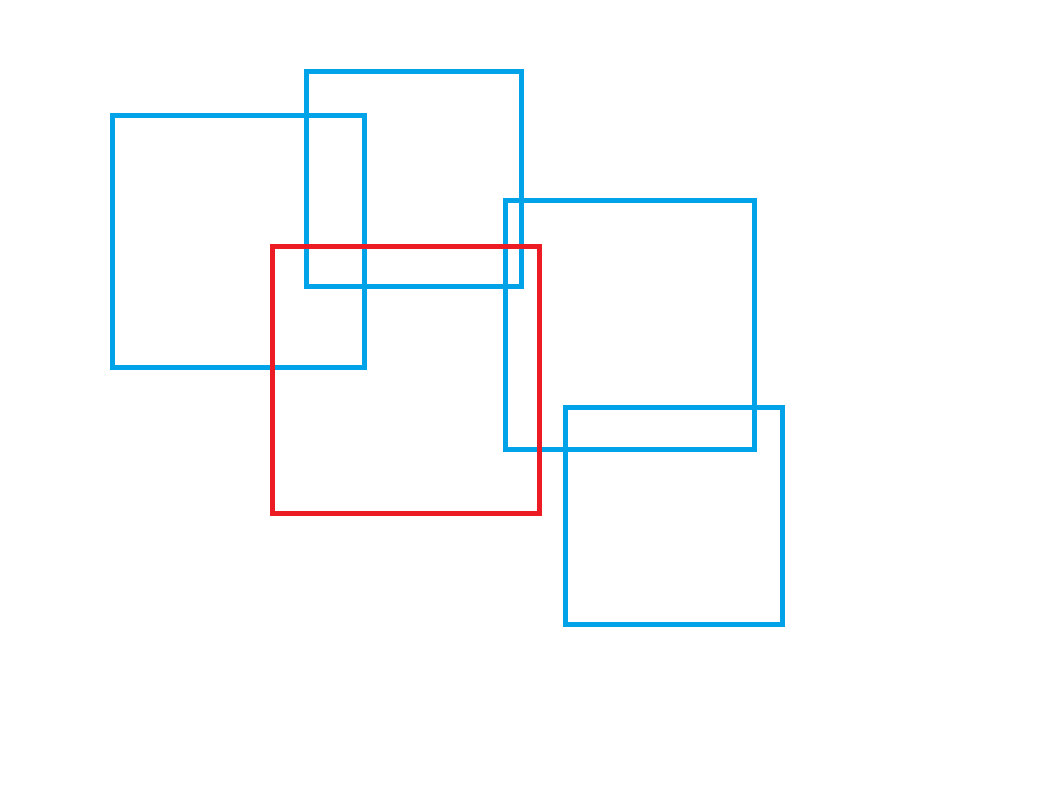
如果我所在的红色矩形没有被完全包含，那么我就是有一丝生机的，反之活不下去。

所以我们利用扫描线先算一下面积并，然后加进去红色矩形再算一次面积并，看一下两个面积并是否有差，如果没有说明死亡。

时间复杂度 O(n\log n)

Code:

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
using namespace std;
#define ll long long
#define ri int

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    ri v = getchar();
    T f = 1;
    t = 0;

    while (!isdigit(v)) {
        if (v == '-')
            f = -1;

        v = getchar();
    }

    while (isdigit(v)) {
        t = t * 10 + v - 48;
        v = getchar();
    }

    t *= f;
}
template <typename T, typename... Args> inline void read(T &t, Args &... args) {
    read(t);
    read(args...);
}

const int N = 1e5 + 10;
const int M = 2e6 + 10;
const int delta = 1e6 + 1;

int n,kas,js,SZ,rt;
struct mummy {
    int x, y;
} mu[N];
struct line {
    int x, l, r, op;
} seg[N << 1];
struct node {
    int ls, rs;
    ll v, lz;
} tr[N * 40];

bool cmp(line l1, line l2) {
    return l1.x < l2.x;
}
void up(int x, int s, int t) {
    if (tr[x].lz)
        tr[x].v = t - s + 1;
    else if (s == t)
        tr[x].v = 0;
    else
        tr[x].v = tr[tr[x].ls].v + tr[tr[x].rs].v;
}
void ins(int l, int r, int s, int t, int &x, ll num) {
    if (!x)
        x = ++SZ, tr[x].v = tr[x].lz = tr[x].ls = tr[x].rs = 0;

    if (l <= s && t <= r) {
        tr[x].lz += num, up(x, s, t);
        return;
    }

    int mid = (s + t) >> 1;

    if (l <= mid)
        ins(l, r, s, mid, tr[x].ls, num);

    if (mid + 1 <= r)
        ins(l, r, mid + 1, t, tr[x].rs, num);

    up(x, s, t);
}
int check(int T) {
    js = SZ = rt = 0;
    ll orz = 0;

    for (int i = 1; i <= n; ++i) {
        int X1 = max(-T, mu[i].x - T), X2 = min(T, mu[i].x + T);
        int Y1 = max(-T, mu[i].y - T), Y2 = min(T, mu[i].y + T);

        if (X1 > X2 || Y1 > Y2)
            continue;

        seg[++js] = (line) {X1, Y1, Y2, 1}, seg[++js] = (line) {
            X2 + 1, Y1, Y2, -1
        };
    }

    sort(seg + 1, seg + 1 + js, cmp);

    for (int i = 1; i <= js; ++i) {
        if (i != 1)
            orz += 1LL * (seg[i].x - seg[i - 1].x) * tr[rt].v;

        ins(seg[i].l, seg[i].r, -M, M, rt, seg[i].op);
    }

    return orz >= 1LL * (T + T + 1) * (T + T + 1);
}

signed main() {
    while (1) {
        read(n), ++kas;

        if (n == -1)
            break;

        for (int i = 1; i <= n; ++i) read(mu[i].x,mu[i].y);

        int l = 1, r = 1000000, ans = -1;

        while (l <= r) {
            int mid = (l + r) >> 1;

            if (check(mid))
                ans = mid, r = mid - 1;
            else
                l = mid + 1;
        }

        printf("Case %d: ", kas);

        if (ans == -1)
            puts("never");
        else
            printf("%d\n", ans);
    }

    return 0;
}

K

给出一个简单多边形，求最小宽度

n \leq 100

注意到你一个宽度是可以有两条平行直线确定的，最优方案肯定存在一种让直线和多边形一边重合的，所以大力扫一下就完事了。

网上一车人用了旋转卡壳，其实不用。

Code:

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
using namespace std;
#define ll long long
#define ri int

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    ri v = getchar();T f = 1;t = 0;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
    t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
    read(t);read(args...);
}

const int N = 110;

struct Point
{
    double x,y;
    Point(double x=0,double y=0):x(x),y(y){ }
}p[N];

typedef Point Vector;
const double esp = 1e-10;

int dcmp(double x) {if(fabs(x) < esp) return 0; else return x<0?-1:1;}

Vector operator + (Vector A, Vector B) {return Vector(A.x+B.x, A.y+B.y);}
Vector operator - (Vector A, Vector B) {return Vector(A.x-B.x, A.y-B.y);}
Vector operator * (Vector A, double p) {return Vector(A.x*p, A.y*p);}
Vector operator / (Vector A, double p) {return Vector(A.x/p, A.y/p);}
bool operator < (const Point& a, const Point& b){ return a.x<b.x || (a.x==b.x && a.y<b.y);}
bool operator == (const Point& a, const Point& b){return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;}

double Dot(Vector A, Vector B){ return A.x*B.x+A.y*B.y; }
double Length(Vector A){return sqrt(Dot(A, A));}
double Angle(Vector A, Vector B) {return acos( Dot(A, B)/Length(A)/Length(B) );}

double Cross(Vector A, Vector B) { return A.x*B.y - A.y*B.x ;}
double Area2(Point A, Point B, Point C){return Cross(B-A, C-A); }

double DistanceToLine(Point P, Point A, Point B)
{
    Vector v1 = B-A, v2 = P-A;
    //cout << fabs(Cross(v1, v2)) << " " << Length(v1) << " " << fabs(Cross(v1, v2)) / Length(v1) << endl;
    return Cross(v1, v2) / Length(v1);
}

int n,$;

signed main() {
    while (cin >> n) {
        if (!n) return 0;
        for (int i = 1;i <= n;++i) cin >> p[i].x >> p[i].y;
        double minn = 1e20;
        for (int i = 1;i <= n;++i) {
            for (int j = i + 1;j <= n;++j) {

                Point l = p[i],r = p[j];

                double maxdis = 0,mindis = 0;
                for (int k = 1;k <= n;++k) {
                    if (k != i && k != j) {
                            //printf("%d %d %lf\n",i,j,DistanceToLine(p[k],l,r));
                            maxdis = max(maxdis,DistanceToLine(p[k],l,r));
                            mindis = min(mindis,DistanceToLine(p[k],l,r));
                        //cout << maxdis << " " << mindis << endl;
                    }
                }
                minn = min(minn,maxdis-mindis);
            }
        }
        minn = ceil(minn * 100) / 100.0;
        printf("Case %d: %.2lf\n",++$, minn);
    }
    return 0;
}

2011 ACM-ICPC World Finals 解题报告

A

思考题

C

E

Code:

F

G

H

Code:

J

Code:

I

Code:

K

Code:

评论已关闭

热门文章

最新文章

分类

标签

其它