P7594 「EZEC-8」Clear Up

首先先研究一下 a_i \not ={0} 的情况，我们先把操作记为 (l_1,r_1),(l_2,r_2) 显然两个操作的代价分别是 \frac{l_1 + r_1}{2},\frac{l_2 + r_2}{2}

可以证明，如果 (l_1,r_1),(l_2,r_2) 有交集，结果肯定不如选 (\min(l_1,l_2),\max(r_1,r_2)) 来的优。

简要证明一下：

第一种情况：(l_2,r_2) \in (l_1,r_1) 如图：

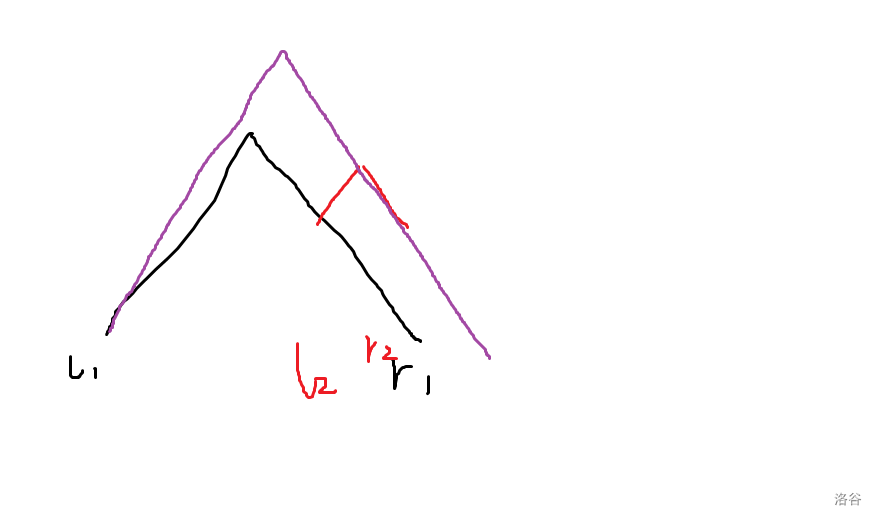
这里，选紫色的覆盖方式代价与 (l_1,r_1),(l_2,r_2) 的代价相同，但是可以覆盖到更多的数。

第二种情况：(l_2,r_2) \notin (l_1,r_1)

同上。

所以我们不难写出 45 分代码：

int las,nxt;++n;
for (int i = 1;i <= n;++i) {
    if (a[i] && !a[i-1]) {
        las = i;
        continue;
    }
    if (!a[i]) {
        if (!a[i-1]) continue;
        nxt = i - 1;
        ll tmp = 0x3f3f3f3f3f3f3f3f;
        pre[las] = a[las] - las;suf[nxt] = a[nxt] + nxt;
        for (int j = las + 1 ;j <= nxt;++j) pre[j] = max(pre[j-1],a[j] - j);
        for (int j = nxt - 1 ;j >= las;--j) suf[j] = max(suf[j+1],a[j] + j);
        for (int j = las ;j <= nxt;++j) tmp = min(tmp,max(pre[j] + j,suf[j] - j));
        ans += tmp;
    }
}

该算法的核心在于找出前缀最大后缀最大，然后选择这个位置。

那么存在 0 的时候，显然整个东西会被分成若干个段，这些段之间选的点可能有交集，所以不能直接算。

但是交集启发我们可以通过判断区间交来合并，我们利用一个栈来完成这个工作，每做完一个非 0 段之后就把区间与栈里的能合并的区间都合并到一起，代码很好写，时间复杂度 O(n)。

pii s[N];

int top,n,L,R;
ll ans;

signed main() {
    read(n);
    for (int i = 1;i <= n;++i) {
        int x;read(x);
        if (!x) continue;
        int l = i - x,r = i + x;
        if (l > R) {
            s[++top] = make_pair(L,R);
            L = l,R = r;
        } else {
            L = min(L,l),R = max(R,r);
            while (L <= s[top].second && top) {
                L = min(L,s[top--].first);
            }
        }
    }
    s[++top] = make_pair(L,R);
    for (int i = 1;i <= top;++i) ans += (ll)(s[i].second - s[i].first + 1) / 2;
    printf("%lld\n",ans);
    return 0;
}

这种方法里使用的是不同的求非 0 段方法，其实是等价的。