P2458 [SDOI2006]保安站岗

有一棵无根树有 n 个点，每个点都可以被其相邻的点望到。

每个点带有一个权值，求保证所有点都可以被望到的情况下花费总代价最少。

解题思路：

树形 DP。

最开始我的想法和树上最小点覆盖的想法一样，每个点有选与不选两种状态，暴力转移。

成功拿到 10 分。

回到正题，这题和树上最小点覆盖的本质区别在于：

  • 树上最小点覆盖每个点只能被父亲看见
  • 本题中的每个点可以被父亲或者儿子看见

所以直接导致我们的状态不再适用。

那么怎么办呢？可以暴力直接把这种情况加进去！

同样，我们设 f_{i,0/1/2} 表示第 i 个点的情况：

  • 如果是 0 ，表示当前点被选中
  • 如果是 1 ，表示当前点是被父亲看到的，且当前点未被选中
  • 如果是 2 ，表示当前点是被儿子看到的，且当前点未被选中

前两种情况的转移方程很好写，考虑可行性即可。

f_{x,0} = \min_{y \in son(x)}(f_{y,0,}f_{y,1},f_{y,2})

因为该点被选中，所以子节点怎么转移都行

f_{x,1} = \min_{y \in son(x)}(f_{y,0},f_{y,2})

因为该点没被选中，所以子节点中 f_{y,1} 就不能被转移。

最后一种情况似乎大同小异：

f_{x,2} = \min_{y \in son(x)}(f_{y,0},f_{y,2})

但是，让我们考虑这样的一种情况：

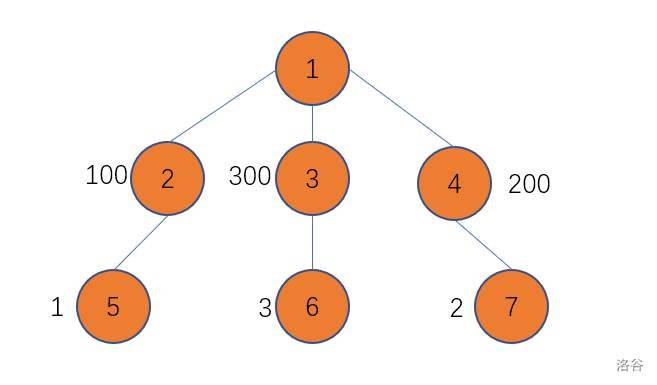
在这张图中，f_{1,2} = f_{2,2}+f_{3,2}+f_{4,2} ，显然不符合状态的定义， 1 并没有被观察到，所以我们还要暴力选择一个f_{y,0}-f_{y,2}差值最小的点（上图中为 2）才能保证正确性。

所以我们就可以写出最后一种情况的方程了：

如果有选择 f_{y,0}，则

f_{x,2} = \min_{y \in son(x)}(f_{y,0},f_{y,2})

如果没有，则

f_{x,2} = \min_{y \in son(x)}(f_{y,0},f_{y,2}) + \min_{y \in son(x)}(f_{y,0} - f_{y,2}))

这两个只要在代码实现时候记录下即可。

初值：f_{x,0} = a_x,f_{x,1} = f_{x,2} = 0

目标：\min(f_{root,0},f_{root,2})（根节点没有父亲，所以没有 f_{root,1} 的情况）

最后，由于并没有指定根，所以读入时还要记一下入度为 0 的点当作根开始 DP。

代码：

省略头文件

int n,a[N],f[N][3],deg[N];
//f_{i,0} 表示当前点放一个 f_{i,1}表示父亲放 f_{i,2} 表示儿子放
//当前点放的话随便转移
//父亲点放的话可以转移到f_{y,0}或f_{y,2}
//儿子放的话要找到一个最小儿子 让放置儿子代价最小

void dfs(int x,int fa) {
    f[x][0] = 1;    
    int del = INF;//记录f_{y,0} - f_{y,2}的最小值
    bool flag = false;//记录是否选择全部不选
    for (int i = hd[x];i;i = nxt[i]) {
        int y = to[i];
        if (y == fa) continue;
        dfs(y,x);
        f[x][0] += std::min(f[y][0],std::min(f[y][1],f[y][2]));//第一种情况更新
        f[x][1] += std::min(f[y][0],f[y][2]);//第二种情况更新
        if (f[y][0] < f[y][2]) {
            f[x][2] += f[y][0];
            flag = true;//选择了f_{y,0}
        }
        else {
            del = std::min(del,f[y][0] - f[y][2]);//计算f_{y,0} - f_{y,2}的最小值
            f[x][2] += f[y][2];
        }
    }   
    if (!flag) {
        f[x][2] += del;//如果没有选择则暴力加上
    }
}

signed main() {
    read(n);
    for (int i = 1;i < n;++i) {
        int x;read(x);int y;read(y);
        addedge(x,y);
        deg[y]++;//记录每个点入度
    }
    int root = 0;
    for (int i = 1;i <= n;++i) if (!deg[i]) root = i;//记录根节点
    dfs(root,0);
    printf("%d\n", std::min(f[root][0],f[root][2]));
    //根节点没有父亲，所以不用转移f_{root,1}
    return 0;
}