CF1336A/CF1337C

有一个有 n 个点的树，以 1 为根，你可以选择 k 个节点，使得这 k 个节点到 1 节点的最短路径中经过的非选择的点最多。

思路：

先约定：
siz_v 为以 v 为根的子树大小，当 v 为叶子节点时，siz_v = 1。。
dep_v 为从根到 v 的最短路径长度（即深度）。

首先我们可以发现，这里每选择一个点是会对它的子树造成影响。
例如这里：

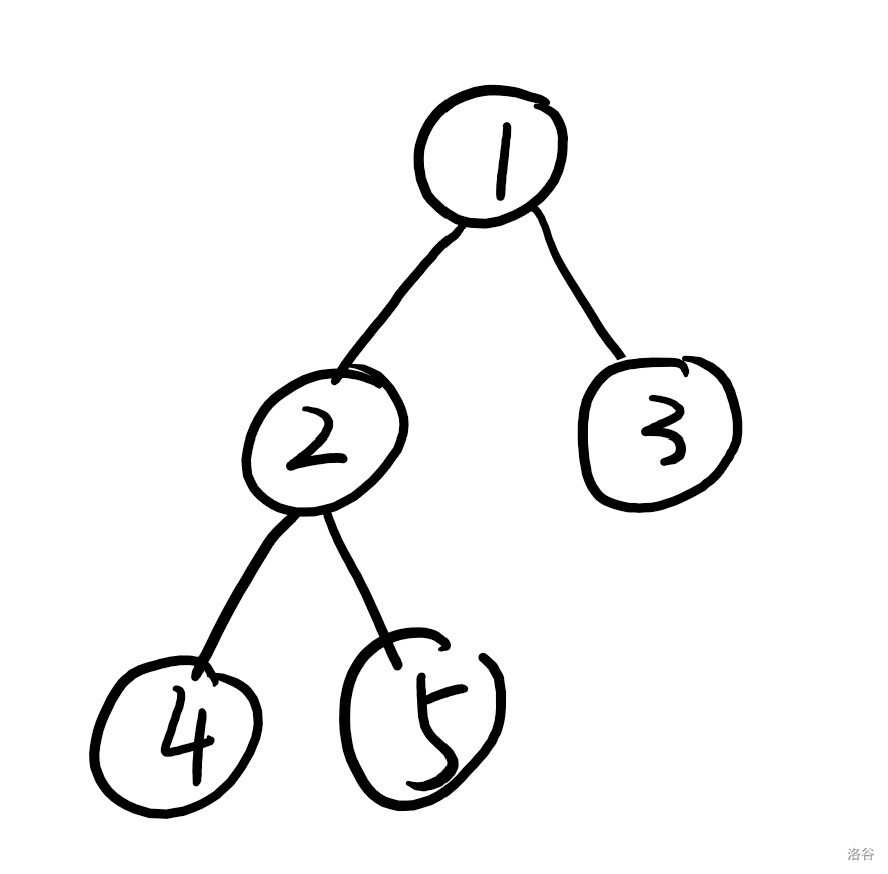
如果我们已经选择了 4,5，那么如果再选择 2， 4,5 到根节点的权值就会各 -1。
所以我们不止要简单的计算深度最大的，而且要计算它的子树大小最小的。
因此，我们设一个点的贡献为 f_v，f_v = dep_v - siz_v,最后对 f_i 排序求出最小的 k 个值相加即可。
显然对于 dep_i 和 siz_i 我们可以通过一遍 DFS 求出来 

void dfs1(int s,int f) {
    a[s].dep = a[f].dep+1,a[s].siz = 1;
    for (int i = hd[s];i;i = nxt[i]) {
        int v = to[i];
        if (v == f) continue;
        dfs1(v,s);
        a[s].siz += a[v].siz;
    }
}

之后就是简单的计算 f_i 的过程了，不再多说。

代码

//本代码是赛时代码，可能有些变量名称不一样，但大体思路一致。
#include <bits/stdc++.h>
using namespace std;
#define int long long//答案会超出int的范围
#define ri register int

inline int read() {
    char v = getchar();int x = 0,f = 1;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {x = x * 10 + v - 48;v = getchar();}
    return x * f;
}

const int N = 500001;
const int M = 500001;

int to[M],hd[N],nxt[M],tot;

inline void add(int u,int v) {to[++tot] = v;nxt[tot] = hd[u];hd[u] = tot;}
inline void addedge(int u,int v) {add(u,v),add(v,u);}

struct node {
    int dep,siz;
}a[N];
//a[i].dep 存的是 dep[i] a[i].siz 存的是 siz[i] 
inline bool cmp(node a,node b) {
    return (a.dep-a.siz)>(b.dep-b.siz);
}
//按照dep[i] - siz[i]（也就是f[i]）排序
void dfs1(int s,int f) {
    a[s].dep = a[f].dep+1,a[s].siz = 1;//计算dep和siz
    for (int i = hd[s];i;i = nxt[i]) {
        int v = to[i];
        if (v == f) continue;
        dfs1(v,s);
        a[s].siz += a[v].siz;
    }
}

int n,k,ans;

signed main() {
    n = read(),k = read();
    for (int i = 1;i < n;++i) {
        int x = read(),y = read();
        addedge(x,y);
    }
    a[0].dep = 0,a[0].siz = 0;
    dfs1(1,0);
    sort(a+1,a+1+n,cmp);//排序
    for (int i = 1;i <= k;++i) {
        ans += (a[i].dep - a[i].siz);
    }//选前k个
    cout << ans;
    return 0;
}