100 + 30 + 70 + 0，rk 32.

\log^2 n 被卡常，哈哈。

A

考虑把 k 分解质因数，设 k = \prod p_i^{c_i}，那么任何一个合法的答案 n 应当满足 \exist c_j < c_i,2c_j \geq c_i。

题目要求的是最小，所以我们并不需要考虑 p_i 以外的质因子，上边的方法已经给出了构造方案，直接构造即可。

ll x,n;
vector <pll> p;

ll ffpow(ll a,ll b) {
    ll ans = 1;
    for (;b;b >>= 1) {
        if (b & 1) ans = ans * a;
        a = a * a;
    }
    return ans;
}

signed main() {
    read(n);
    for (ll i = 2;i * i <= n;++i) {
        if (n % i == 0) {
            ll cnt = 0;
            while (n % i == 0) {++cnt,n /= i;}
            p.push_back(mp(i,cnt));
        }
    }
    if (n > 1) p.push_back(mp(n,1));
    ll ans = 1;
    bool flag = 1;
    for (auto e : p) {
        if (e.second > 1) flag = 0;
        ans *= ffpow(e.first,(e.second + 1) / 2);
    }
    if (flag) puts("-1");
    else printf("%lld\n",ans);
    return 0;
}

B

算法 1

对于 a_i \leq 3 的情况，其实等于一个多重集排列，直接计算即可。

算法 2

题目中给出了一个很强的性质：1 \leq a_i \leq 9，所以我们只需要对 9 种情况进行讨论。

对于 1,5,7 ，由于他们和其他数都互质，所以他们可以去任何位置。最后再考虑。

对于 6，我们发现它与其他数都不互质，无法交换，所以我们把 6 视为分界点，分段进行考虑。

对于 2,4,8 以及 3,9 这些数之间是不能随便移动的，相对顺序相同。两类的数可以交换，记第一类个数为 a，第二类为 b，那么方案数就是 \binom{a}{a+b}，剩下的直接插板法做一下就行了。

const ll mod = 998244353;
const double eps = 1e-10;
const int N = 1e5 + 10;
inline ll add(ll x, ll y) {return (x += y) >= mod ? x - mod : x;}
inline ll dec(ll x, ll y) {return (x -= y) < 0 ? x + mod : x;}
inline ll mul(ll x, ll y) {return (ll)x * y % mod;}
int n;
ll jc[N],inv[N],a[N];

ll ffpow(ll a,ll b) {
    ll ans = 1;
    for (;b;b >>= 1) {
        if (b & 1) ans = mul(ans,a);
        a = mul(a,a);
    }
    return ans;
}

ll C(ll n,ll m) {
    if (n < m) return 0;
    return jc[n] * inv[m] % mod * inv[n-m] % mod % mod;
}

signed main() {
    read(n);
    jc[0] = 1;
    for (int i = 1;i <= n;++i) {
        jc[i] = mul(jc[i-1],i);
    }
    inv[n] = ffpow(jc[n],mod - 2);
    for (int i = n - 1;i >= 0;--i) {
        inv[i] = mul(inv[i + 1],i + 1);
    }

    int tot = 0,x = 0,y = 0,z = 0;
    for (int i = 1;i <= n;++i) {
        int p;read(p);
        if (p == 4 || p == 8 || p == 2) a[++tot] = 2;
        else if (p == 3 || p == 9) a[++tot] = 1;
        else if (p == 1) ++x;
        else if (p == 5) ++y;
        else if (p == 7) ++z;
        else a[++tot] = 6;
    }
    ll ans = mul(C(n,x),mul(C(n-x,y),C(n-x-y,z)));
    int A = 0,b = 0;
    for (int i = 1;i <= tot;++i) {
        if (a[i] == 1) ++A;
        else if (a[i] == 2) ++b;
        else ans = mul(ans,C(A+b,A)),A = b = 0;
    }
    ans = mul(ans,C(A+b,A)),A = b = 0;
    printf("%lld\n",ans);
}

C

算法 1

通过暴力/直觉发现答案具有凹性，直接大力三分出目标值，暴力计算时间复杂度是 \mathcal{O}(n^2\log n) 的。

算法2

思考我们能不能优化查询的过程，我们发现计算权值的本质可以分为两个部分：小于 val 的和大于 val 的。对于两个部分，我们开一个权值线段树维护，每次就查询一下和以及数的个数，时间复杂度 \mathcal{O}(n\log^2 n)。被卡常了。

这里的实现是一种不同于场上实现的较快的三分写法。

const int N = 1e5 + 10;
ll n,a,b,x[N],c[N],qq[N],t[N],cnt,rk[N];
ll f[N];

struct node {
    int l,r;
    ll sum,cnt;
}tree[N<<2];

void build(int p,int l,int r) {
    tree[p].l = l,tree[p].r = r;
    if (l == r) return ;
    int mid = (l + r) >> 1;
    build(p << 1,l,mid);
    build(p << 1 | 1,mid + 1,r);
}

void modify(int p,int pos,ll k) {
    if (tree[p].l == tree[p].r) {
        tree[p].sum += k;
        tree[p].cnt += 1;
        return ;
    }
    int mid = (tree[p].l + tree[p].r) >> 1;
    if (pos <= mid) modify(p << 1,pos,k);
    else modify(p << 1 | 1,pos,k);
    tree[p].sum = (tree[p << 1].sum + tree[p << 1 | 1].sum);
    tree[p].cnt = (tree[p << 1].cnt + tree[p << 1 | 1].cnt);
}

ll query1(int p,int l,int r) {
    if (tree[p].l >= l && tree[p].r <= r) {
        return tree[p].sum;
    }
    int mid = (tree[p].l + tree[p].r) >> 1;
    ll ans = 0;
    if (l <= mid) ans += query1(p << 1,l,r);
    if (r > mid) ans += query1(p << 1 | 1,l,r);
    return ans;
}

ll query2(int p,int l,int r) {
    if (tree[p].l >= l && tree[p].r <= r) {
        return tree[p].cnt;
    }
    int mid = (tree[p].l + tree[p].r) >> 1;
    ll ans = 0;
    if (l <= mid) ans += query2(p << 1,l,r);
    if (r > mid) ans += query2(p << 1 | 1,l,r);
    return ans;
}

ll calc(int val,int pos) {
    ll ans = a *((qq[val] * query2(1,1,val)) - (query1(1,1,val)));
    ans += b * (query1(1,val + 1,cnt) - (query2(1,val+1,cnt) * qq[val]));
    return ans;
}

ll solve(int pos) {
    int l = 1,r = cnt;
    ll lans = 0,rans = 0,ans = 1e18;

    while ((l + 1) < r) {
        int mid = (l + r) >> 1;
        ll ans1 = calc(mid - 1,pos),ans2 = calc(mid + 1,pos);
        if (ans1 > ans2) l = mid;
        else r = mid;
    }
    //printf("pos:%d\n",l);
    return min(calc(l,pos),calc(r,pos));
}

signed main() {
    //FO(test)
    read(n,a,b);
    for (int i = 1;i <= n;++i) read(x[i]),c[i] = x[i];
    sort(c+1,c+1+n);
    for (int i = 1;i <= n;++i) if (c[i] != c[i-1]) qq[++cnt] = c[i];
    for (int i = 1;i <= n;++i) t[i] = lower_bound(qq + 1,qq + 1 + cnt,x[i]) - qq;
    build(1,1,cnt);
    for (int i = 1;i <= n;++i) {
        modify(1,t[i],x[i]);
        printf("%lld\n",solve(i));
    }
    return 0;
}

算法3

线段树部分到头了，我们考虑两个点变化的时候挪动的个数非常有限，事实上可以证明至多只会变 1。所以我们时间复杂度就是 \mathcal{O}(n\log n)。贴一个其他老哥写的 code

#include<bits/stdc++.h>
using namespace std;

#define MAXN 200005
#define int long long 

int n;
int x[MAXN],a,b;
int ans;

priority_queue<int> down;
priority_queue<int,vector<int>,greater<int> >up;
int sumup,sumdown;

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cin>>n>>a>>b;
    int cnt=0,l=0;
    for(int i=1; i<=n; i++) cin>>x[i];
    for(int i=1; i<=n; i++) {
        if(x[i]>l) {
            up.push(x[i]);
            sumup+=x[i];
        } else {
            int w=down.top();down.pop();sumdown-=w;
            up.push(w);sumup+=w;
            down.push(x[i]);sumdown+=x[i];
        }
        int k=(i*b)/(a+b)+1;
        while(cnt<k) {
            int w=up.top();up.pop();sumup-=w;
            down.push(w);sumdown+=w;cnt++;
        }
        l=down.top();
        ans=(cnt*l-sumdown)*a+(sumup-(i-cnt)*l)*b;
        cout<<ans<<"\n";
    }
    return 0;
}

D

我们考虑这个东西怎么分开来计算，显然对于一个 (x,y)，我们计算的部分可以这么构成：

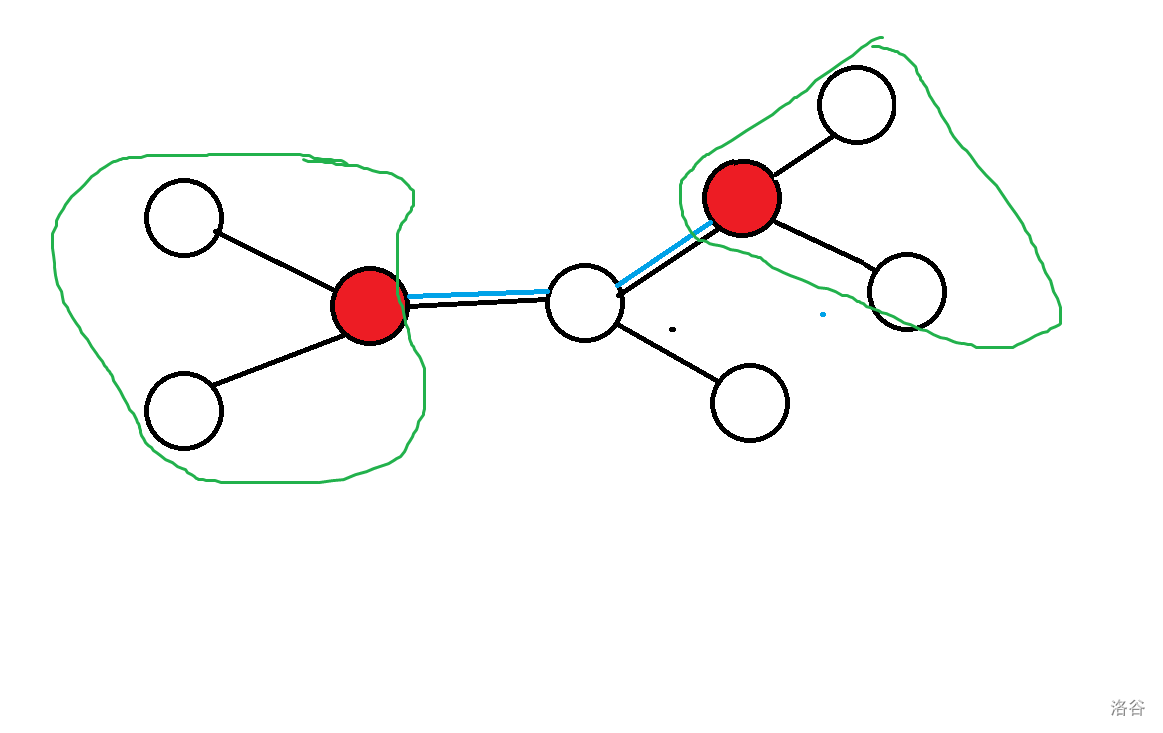
我们记 f_{x,y} 表示树根为 y,以 x 为根的子树内答案，那么答案就是 f_{x,y} \times f_{y,x} \times dis_{x,y}，暴力计算是 \mathcal{O}(n^2 q) 的，我们考虑优化这个过程。

首先我们考虑，实际上我们并不是对于每一种询问都需要重新计算 f，只有一种情况我们需要特殊考虑：x 在 y 的子树内，以下我们称这种情况为包含情况。

对于不包含情况，我们实际上不需要处理额外的 f，我们直接按照定义处理出 f_{x,1} 然后相乘就行了。正确性是显然的。

对于包含情况，可以看图理解一下：

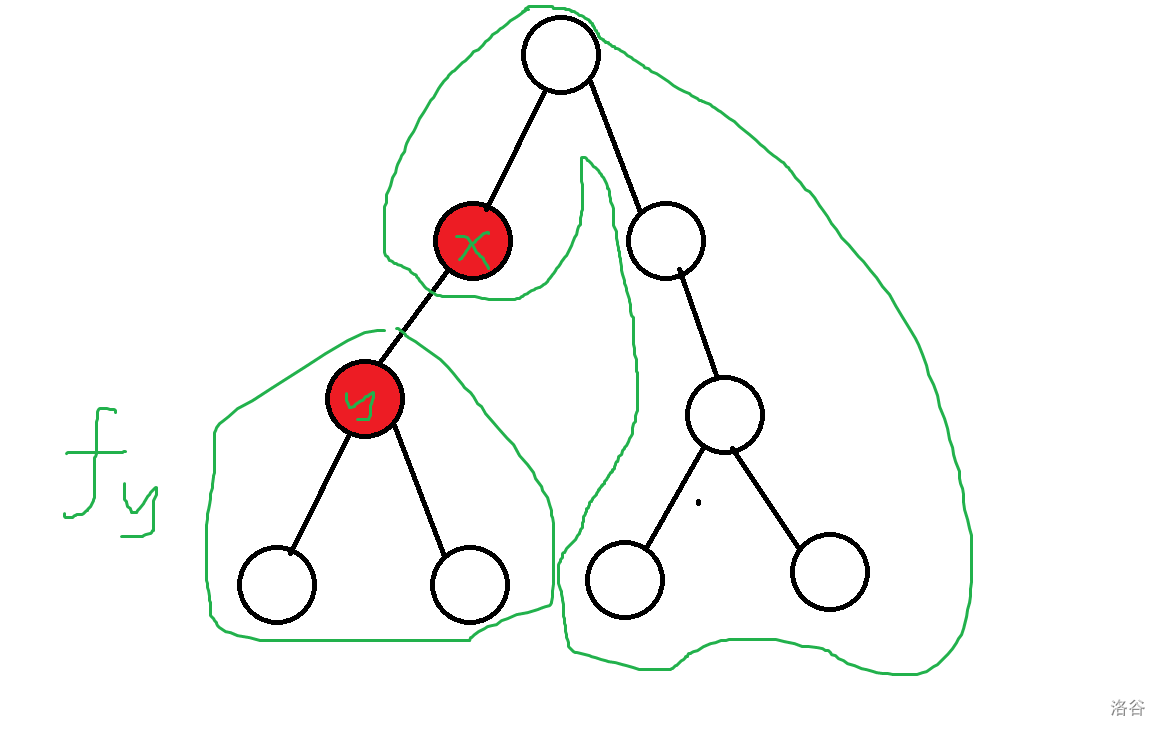
我们要计算的答案显然是两个绿色部分相乘，那么我们发现常规来计算 x 的贡献是相对困难的，我们需要额外处理的是一个 g，它表示以当前节点 x 的父亲为根时，除了 x 子树内的答案。那么我们首先应该找到 y 对应的 x 的子树是哪一棵，这个我们可以通过暴力跳重链在 \mathcal{O}(\log n) 的时间内做到。然后就统计一下即可。实现到代码是这样的：

int get(int x,int y) {
    while (top[x] != top[y]) {
        if (fat[top[x]] == y) return top[x];
        x = fat[top[x]];
    }
    return rk[dfn[y] + 1];
}
if (lca == x) {
    printf("%d %d\n",get(y,x),g[get(y,x)]);
    ans = mul(mul(g[get(y,x)],f[y]),dis);
} else {
    ans = mul(mul(f[x],f[y]),dis);
}

所以我们就在 \mathcal{O}((n + q)\log n) 的时间内解决了问题，如果想要更快需要 tarjan 求 LCA，但是我猜没几个人写。

inline int add(int x, int y) {return (x += y) >= mod ? x - mod : x;}
inline int del(int x, int y) {return (x -= y) < 0 ? x + mod : x;}
inline int mul(int x, int y) {return (ll)x * y % mod;}
const int N = 1e6 + 10;
int n,q,dep[N],fat[N],tag[N],ans1,ans2,f[N],g[N],top[N],son[N],siz[N],dfn[N],rk[N],cnt;
vector <int> G[N];

ll ffpow(ll a,ll b) {
    ll ans = 1;
    for (;b;b >>= 1) {
        if (b & 1) ans = mul(ans,a);
        a = mul(a,a);
    }
    return ans;
}

void dfs(int x,int fa) {
    dep[x] = dep[fa] + 1;
    siz[x] = 1;
    fat[x] = fa;
    son[x] = 0;
    for (auto y : G[x]) {
        if (y != fa) {
            dfs(y,x);
            siz[x] += siz[y];
            if (siz[y] > siz[son[x]]) son[x] = y;
        }
    }
}

void dfs1(int x,int fa) {
    dfn[x] = ++cnt,rk[cnt] = x;
    if (son[fa] != x) top[x] = x;
    else top[x] = top[fa];
    if (son[x]) dfs1(son[x],x);
    else return ;
    for (auto y : G[x]) {
        if (y != fa && y != son[x]) {
            dfs1(y,x);
        }
    }
}

int LCA(int x,int y) {
    while (top[x] != top[y]) {
        if (dep[top[x]] < dep[top[y]]) swap(x,y);
        x = fat[top[x]];
    }
    return dep[x] < dep[y] ? x : y;
}

void dfs2(int x,int fa) {
    f[x] = 1;
    for (auto y : G[x]) {
        if (y != fa) {
            dfs2(y,x);
            f[x] = add(f[x],mul(2,f[y]));
        }
    }
}

void dfs3(int x,int fa) {
    for (auto y : G[x]) {
        if (y != fa) {
            g[y] = del(add(f[x],add(g[x],g[x])),add(f[y],f[y]));
            dfs3(y,x);
        }
    }
}

int get(int x,int y) {
    while (top[x] != top[y]) {
        //printf("%d %d\n",top[x],top[y]);
        if (fat[top[x]] == y) return top[x];
        x = fat[top[x]];
    }
    return rk[dfn[y] + 1];
}

signed main() {
    read(n);
    for (int i = 1;i < n;++i) {
        int x,y;read(x,y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    dfs(1,0);
    dfs1(1,0);
    dfs2(1,0);
    dfs3(1,0);
    read(q);
    for (int i = 1;i <= q;++i) {
        int x,y;read(x,y);
        int lca = LCA(x,y);
        if (dep[x] > dep[y]) swap(x,y);
        int dis = ffpow(2,dep[x] + dep[y] - 2 * dep[lca]);
        ll ans = 0;
        if (lca == x) {
            printf("%d %d\n",get(y,x),g[get(y,x)]);
            ans = mul(mul(g[get(y,x)],f[y]),dis);
        } else {
            ans = mul(mul(f[x],f[y]),dis);
        }
        printf("%d\n",ans);
    }   
}