正睿前先提前入狱坐会牢。

Round 1

C

二维平面，屏幕是 (0, 1)–(0, m) 的线段

有 n 行 m 列座位在屏幕前面，是坐标范围 1 ≤ x ≤ n, 1 ≤ y ≤ m 的整点

有 k 个座位已经有人，求出到屏幕的视线不被任何人挡住的座位数量

q 次询问，每次修改一个人的坐标后求出答案

2 ≤ n, m ≤ 2 \times 10^5 , 1 ≤ k ≤ 2 \times 10^5 , 1 ≤ q ≤ 200

观察到范围，本题是想让我们在 \mathcal{O}(nq) 的时间内解决问题。

我们先思考一下一个人能挡住他人的情况，记这个人在 x 行 y 列：

1. 当 y = 1 或者 y = m 的时候，一个人只会挡住其右边的点，如下：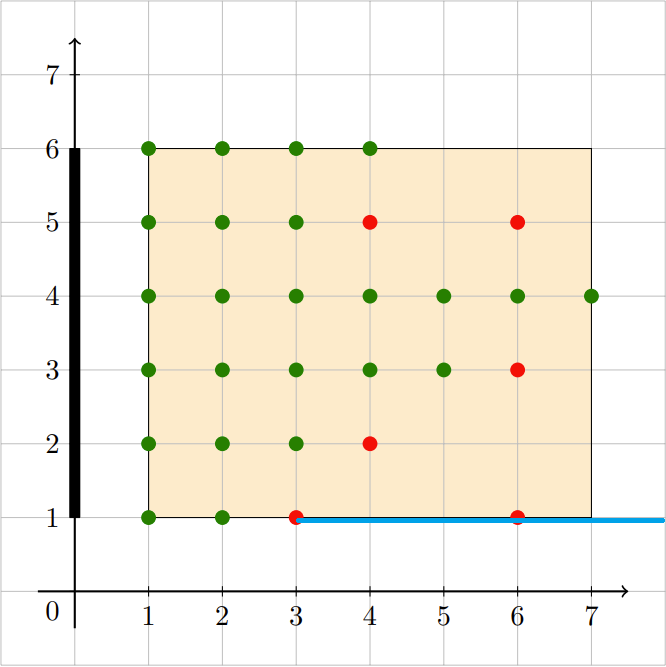

   

2. 当 1 < y < m 时，我们要考虑的可以分成两部分：从 (0,1) 引出的射线涵盖的地方，从 (0,m) 引出的射线涵盖的地方，求个并集就 OK。

这两种情况其实是对称的，一种的斜率大于 0 另一种小于 0，我们接下来讲解以 (0,1) 射线统计为例，(0,m) 情况统计同理。我们对射线的斜率进行考虑，很显然，斜率大的射线会覆盖掉斜率小的射线如下：

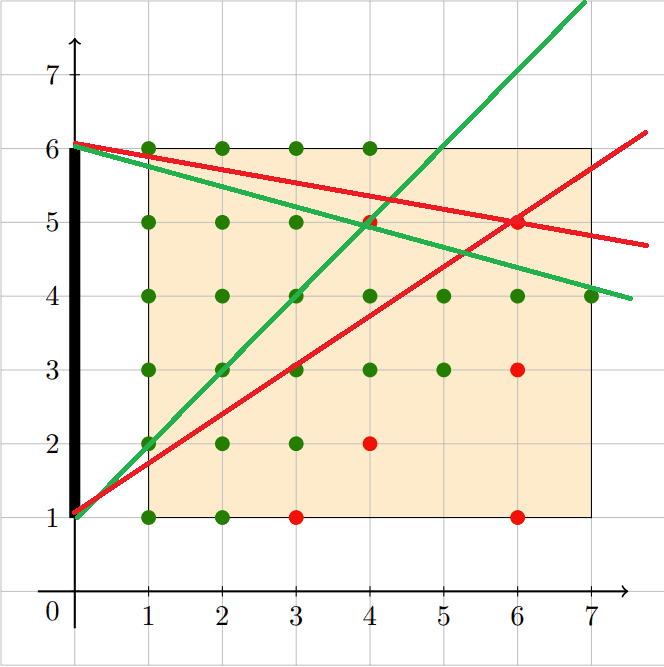
接下来我们发现，对于一行来说，我们只需要考虑最前面的 x，小的位置会覆盖大的，这个和上面的道理是一样的。

所以我们从小到大处理，维护最大斜率，我们就能得出每一列的答案，(0,m) 的就是从大到小考虑。

这样的总时间复杂度为 \mathcal{O}(nq)

const int N = 2e5 + 10;

int n,m,k,q;
int x[N],y[N],pos[N];
vector <int> buc[N];

bool cmp(int x1,int y1,int x2,int y2) {
    return y2 * x1 < y1 * x2;
}

signed main() {
    read(n,m,k,q);
    for (int i = 1;i <= k;++i) read(x[i],y[i]);
    for (int i = 1;i <= q;++i) {
        int num;read(num);
        read(x[num],y[num]);
        for (int j = 1;j <= m;++j) buc[j].clear(),pos[j] = n + 1;
        for (int j = 1;j <= k;++j) buc[y[j]].push_back(x[j]);
        int xx = -1,yy = 0;
        for (int j = 1;j <= m;++j) {
            if (j == 1) {
                for (auto x : buc[j]) {
                    pos[j] = min(pos[j],x);
                }
                continue;
            }
            for (auto x : buc[j]) {
                if (cmp(xx,yy,j-1,x)) xx = j-1,yy = x;
            }
            if (yy) {
                int nowx = (ll)((j - 1) * yy + xx - 1) / xx;
                pos[j] = min(pos[j],nowx);
            }
            //puts("here");
        }
        xx = -1,yy = 0;
        for (int j = m;j >= 1.;--j) {
            if (j == m) {
                for (auto x : buc[j]) {
                    pos[j] = min(pos[j],x);
                }
                continue;
            }
            for (auto x : buc[j]) {
                if (cmp(xx,yy,m-j,x)) xx = m-j,yy = x;
            }
            if (yy) {
                int nowx = ((m-j) * yy + xx - 1) / xx;
                pos[j] = min(pos[j],nowx);
            }
        }
        ll ans = 0;
        for (int j = 1;j <= m;++j) ans += pos[j] - 1;
        printf("%lld\n",ans);
    }
    return 0;
}

J

有一张 n 个点 m 条边的无重边无自环的有向图

初始时可以选择一个点染黑，其余点均为白点

若某个点所有入边的起点均为黑点，则该点可以被染黑

最大化图中黑点数量

1 ≤ ∑n ≤ 2 × 10^5 , 1 ≤ ∑m ≤ 5 × 10^5

这个题建反图会更加直观。

一个点覆盖意味着前驱点都被覆盖，考虑贪心，如果遇到一个点的入度是 1，那么我们把这相应的两个点进行缩点，把两个点的信息合在一起，最后统计最大的点的大小就能得出答案，这里我们采用并查集维护。

朴素合并的复杂度是 \mathcal{O}(n^2\log n )，考虑怎么优化。

我们发现这里同样可以应用启发式合并，每次把大的集合信息同步到小的集合信息上，就可以把复杂度变为 \mathcal{O}(n\log^2 n) 的了。

题解还将了个随机化做法，这个比较逆天，不是很会，有兴趣可以自己研究（

const int N = 2e5 + 10;

int n,f[N],siz[N],cas;
set <int> G1[N],G2[N];
int find(int x) {
    return f[x] == x ? x : f[x] = find(f[x]);
}

void dfs(int u,int v) {
    int fx = find(u),fy = find(v);
    if (fx == fy) return ;
    if (G2[fx].size() > G2[fy].size()) swap(fx,fy);
    vector <pii> edg;
    for (auto y : G2[fx]) {
        G2[fy].insert(y);
        G1[y].erase(fx);
        G1[y].insert(fy);
        if (G1[y].size() == 1) edg.push_back(mp(fy,y));
    }
    f[fx] = fy;
    siz[fy] += siz[fx];
    for (auto p : edg){
        dfs(p.first,p.second);
    }
}

void solve() {
    read(n);++cas;
    for (int i = 1;i <= n;++i) G1[i].clear(),G2[i].clear(),f[i] = i,siz[i] = 1;
    for (int i = 1;i <= n;++i) {
        int k;read(k);
        for (int j = 1;j <= k;++j) {
            int y;read(y);
            G1[i].insert(y);G2[y].insert(i);
        }
    }
    for (int i = 1;i <= n;++i) {
        if (G1[i].size() == 1) {
            dfs(i,*G1[i].begin());
        }
    }
    int ans = 0;
    for (int i = 1;i <= n;++i) ans = max(ans,siz[i]);
    printf("Case #%d: %d\n",cas,ans);
}

signed main() {
    int T;read(T);
    while (T--) solve();
    return 0;
}

Round 2

D

有一家商店，在这家商店里有 n 个物品和 m 条交易方法，对于每条交易方法，你可以用 k \times a_i 的 b_i 类物品换到 k\times w \times c_i 的 d_i 类物品（其中 k，w 是任意正实数）

请求出最小的 w 使得不会产生无限个物品。

n \leq 1000,m \leq 2000

这个题比较 trivial,我们把图建出来，每一个方法对应 b_i\rightarrow d_i 边权为 \frac{w\times c_i}{a_i} 的边，那么产生无限个物品当且仅当图里存在一个边权乘积大于 1 的环。

注意到直接套 SPFA 求的话精度上会寄（有人 -11 我不说是谁），所以运用一个常见技巧，也就是取 \log 把边权变为 \log {c_i} - \log {a_i}，外边套个二分做一下，总时间复杂度就是 \mathcal O(SPFA(n)\log ^2 n)

//Every night that summer just to seal my fate
//And I scream, "For whatever it's worth
//I love you, ain't that the worst thing you ever heard?"
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define mp make_pair

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    int v = getchar();T f = 1;t = 0;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
    t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
    read(t);read(args...);
}

const double eps = 1e-7;
const int N = 2e5 + 10;
int n,m;
int b[N],d[N];
double a[N],c[N];

vector <int> G[N];
vector<pair<int,double> > edges;
int cnt[N],tot[N];
double dis[N];
bool vis[N];
queue <int> q;

bool SPFA(int s,double val) {
    q.push(s);
    vis[s] = 1;dis[s] = 0.0;
    while (!q.empty()) {
        int x = q.front();q.pop();
        vis[x] = 0;
        for (auto i : G[x]) {
            pair<int,double> e = edges[i];
            int y = e.first;double w = e.second-log(val);
            //printf("%Lf %Lf %Lf\n",dis[y],dis[x],w);
            if (dis[y] > dis[x] + w) {

                dis[y] = dis[x] + w;
                if (!vis[y]) {

                if (++cnt[y] >= n) return 1;
                    vis[y] = 1,q.push(y);
                }
            }
        }
    }
    return 0;
}

bool check(double val) {
    memset(vis,0,sizeof vis);
    memset(cnt,0,sizeof cnt);
    for (int i = 1;i <= n;++i) dis[i] = 1e4;
    bool flag =0;
    for (int i = 1;i <= n;++i) {
        if (dis[i] - 1e4 < eps) {
            flag = SPFA(i,val);
            //printf("%d:",i);
            if (flag) return 1;
        } 
    }

    return 0;
}

signed main() {
    read(n,m);
    for (int i = 1;i <= m;++i) {
        read(a[i],b[i],c[i],d[i]);
        double aa = log(a[i]),cc = log(c[i]);
        edges.push_back(mp(d[i],aa-cc));
        G[b[i]].push_back(edges.size()-1);
    }
    double l = eps,r = 1.00000000;
    while (r - l > eps) {
        double mid = (l + r) / 2.0;
        //printf("%lf\n",mid);
        if (!check(mid)) l = mid;
        else r = mid;
    }
    printf("%.8lf",l);
    return 0;
}

L

有 n 个世界，每个世界是一张简单有向图。

从这些世界中选择一个子段进行游戏，规则为从 1 出发，每个世界可以原地不动或经过一条边，到达点 m 即为胜利。

要求选出一个尽可能短的子段，使得存在至少一种方案可以胜利。

n \leq 10 ^4,m \leq 2\times 10^3 空间限制为 32MB

有人是演员，我不说是谁

观察到这是个分层图，以及这个子段的限制乍看一下非常吓人。但是观察一下空间限制就能发现这个题实际上是个诈骗题（但是我场上没发现）

大力设计 DP 状态，定义 f_{i,j} 表示在第 i 个世界到达第 j 点，最晚可以从哪个世界出发。

DP 的时候类似建反图（但是这里不需要建出显式图），有：

f_{i,1} = i\\ f_{i,j} = \max_{world_{i-1} k\rightarrow j} f_{i-1,k}

//Every night that summer just to seal my fate
//And I scream, "For whatever it's worth
//I love you, ain't that the worst thing you ever heard?"
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define mp make_pair

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    int v = getchar();T f = 1;t = 0;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
    t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
    read(t);read(args...);
}

const int N = 1e4 + 10;

int f[2][N],n,m,ans;

signed main() {
    read(n,m);
    int now = 1,lst = 0;
    ans = n + 1;f[0][1] = 1;
    for (int i = 1;i <= n;++i) {
        swap(now,lst);
        for (int j = 1;j <= m;++j) f[now][j] = f[lst][j];
        int l;read(l);
        for (int j = 1;j <= l;++j) {
            int x,y;read(x,y);
            f[now][y] = max(f[now][y],f[lst][x]);
            if (x == 1) f[now][y] = i;
        }
        if (f[now][m]) ans = min(ans,i - f[now][m] + 1);
    }
    if (ans == n+1) puts("-1");
    else printf("%d\n",ans);
    return 0;
}

H

k 层楼，n 个人，第 i 个人想从 a_i 楼到 b_i 楼。

电梯同一时间最多载 m 人，每一时间单位走一层，可以随时向下，但只能到 1 楼才能向上。

求最短时间使得所有人到达他/她想去的楼层。

n, m ≤ 2 × 10^5 , k ≤ 10^9

我们实际上只需要统计一个东西：一个楼层向上会被经过多少次，向下会被经过多少次。

对于向上来说，假设从 a_i 进入，从 b_i 出，那么就是 [a_i,b_i] 全部 +1，这个可用差分来做成单点修改。对于向下来说同理，我们只需要做个前缀和就可以了。

我们记第 i 层向上人数为 f_1(i)，向下人数为 f_2(i)，那么电梯就至少要到达 i+1 层 \lceil \frac{\max\{f_1(i),f_2(i)\}}{m}\rceil 次。

总共要到达的次数就是一个后缀最大值，这个的意义是非常显然的，最后再对这个后缀最大值求一个前缀和，时间复杂度为 \mathcal{O}(k)。

离散化一下，时间复杂度就变成了 \mathcal{O}(n\log n)

//Every night that summer just to seal my fate
//And I scream, "For whatever it's worth
//I love you, ain't that the worst thing you ever heard?"
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define mp make_pair

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    int v = getchar();T f = 1;t = 0;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
    t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
    read(t);read(args...);
}

const int N = 2e5 + 10;

int n,m,k,a[N],b[N],pre[N],suf[N],sufmax[N];
vector <int> c;

signed main() {
    read(n,m,k);
    for (int i = 1;i <= n;++i) read(a[i],b[i]),c.push_back(a[i]),c.push_back(b[i]),c.push_back(a[i]-1),c.push_back(b[i]-1);
    c.push_back(1);
    sort(c.begin(),c.end());
    c.erase(unique(c.begin(),c.end()),c.end());
    int tot = c.size();

    for (int i = 1;i <= n;++i) {
        int l = lower_bound(c.begin(),c.end(),a[i]-1) - c.begin() + 1;
        int r = lower_bound(c.begin(),c.end(),b[i]-1) - c.begin() + 1;

        if (l < r) pre[l]--,pre[r]++;
        else suf[l]++,suf[r]--;
    }
    int now = 0;
    int ans = 0;
    for (int i = tot - 1;i >= 1;--i) {
        ans += (c[i] - c[i-1] - 1) * now;
        pre[i] += pre[i + 1];
        suf[i] += suf[i + 1];
        now = max(now,(max(pre[i],suf[i]) + m - 1) / m);
        ans += now;
        if (c[i-1] == 1) break;
    }
    printf("%d\n",2 * ans);
    return 0;
}

I

每个功夫大师有能力值和技能值，都为向量；

功夫大师们要互相学习技能，一个功夫大师学习后的技能值为所有功夫 大师技能值的加权和；

两个功夫大师间的学习效率（学技能的加权权值）为能力值的余弦相似度；

求所有功夫大师学习后的技能值。

功夫大师的数量不超过 10^4，所有向量长度不超过 50

考虑直接嗯做时间复杂度是 \mathcal{O}(n^2d) 的，如何优化？

我们不妨把式子给展开一下：

Y^{ans}_{i} = \sum\limits_{j = 1}^{n} \frac{X_i\cdot X_j}{|X_i|\cdot |X_j|}\times Y_j \\ \text{Define } X^{\prime}_i \text{ as } \frac{X_i}{|X_i|} \\ \begin{aligned} \Rightarrow Y^{ans}_{i,pos} &= \sum\limits_{j =1}^n \sum\limits_{p = 1}^k X^{\prime}_{i,p} \times X^{\prime}_{j,p} \times Y_{j,pos}\\ &= \sum\limits_{p =1}^k X^{\prime}_{i,p} \sum\limits_{j =1}^n X^{\prime}_{j,p}\times Y_{j,pos} \end{aligned}

我们注意到， X^{\prime}_i 是可以预处理的，\sum\limits_{j =1}^n X^{\prime}_{j,p}\times Y_{j,pos} 也是可以在 \mathcal{O}(nkd) 的时间内预处理出来的。

接下来需要做的工作就是求出这两个之后以 \mathcal{O}(nkd) 的时间乘在一起，所以总时间复杂度是 \mathcal{O}(nkd)

//Every night that summer just to seal my fate
//And I scream, "For whatever it's worth
//I love you, ain't that the worst thing you ever heard?"
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cctype>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define mp make_pair

char buf[1 << 20], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 20, stdin), p1 == p2)?EOF: *p1++)
template <typename T> inline void read(T &t) {
    int v = getchar();T f = 1;t = 0;
    while (!isdigit(v)) {if (v == '-')f = -1;v = getchar();}
    while (isdigit(v)) {t = t * 10 + v - 48;v = getchar();}
    t *= f;
}
template <typename T,typename... Args> inline void read(T &t,Args&... args) {
    read(t);read(args...);
}

const int N = 1e4 + 10;
const int M = 55;
int n,k,d;
double x[N][M],y[N][M],yy[N][M];

signed main() {
    read(n,k,d);
    for (int i = 1;i <= n;++i) {
        double sum = 0;
        for (int j = 1;j <= k;++j) {
            read(x[i][j]);
            sum += x[i][j] * x[i][j];
        }
        sum = sqrt(sum);
        for (int j = 1;j <= k;++j) {
            x[i][j] /= sum;
        }
    }
    for (int i = 1;i <= n;++i) {
        for (int j = 1;j <= d;++j) {
            read(y[i][j]);
        }
    }
    for (int i = 1;i <= k;++i) {
        for (int j = 1;j <= d;++j) {
            for (int l = 1;l <= n;++l) {
                yy[i][j] += x[l][i] * y[l][j];
            }
        }
    }
    for (int i = 1;i <= n;++i) {
        for (int j = 1;j <= d;++j) {
            double ans = 0;
            for (int l = 1;l <= k;++l) {
                ans += x[i][l] * yy[l][j];
            }
            printf("%.10lf ",ans);
        }
        puts("");
    }
    return 0;
}